2015-10-16
615
Ø укрупнение периодов:
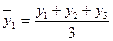
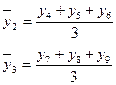
Ø сглаживание динамического ряда при помощи скользящей средней:
; 
; 
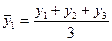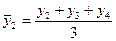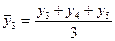и т.д.
Таблица 9– Выравнивание суммы налогов, уплаченных в местный бюджет за 1999-2007 годы с помощью скользящей средней
| Год | Фактическая сумма налогов, уплаченных в местный бюджет, млн. руб. | Сумма по скользящим трехлетиям | Средние скользящие |
| 632,0 661,7 667,3 674,0 675,7 700,7 685,0 |
Ø анализ цепных показателей ряда динамики:
а ) при постоянных цепных абсолютных приростах делается вывод о равномерном типе развития. Основная тенденция в этих рядах выражается уравнением прямолинейной функции yt = a 0 + a 1 t, где
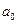и 
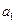– параметры уравнения;
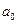– начальный уровень тренда в момент или период, принятый за начало отсчёта времени;
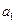– среднее абсолютное изменение за единицу времени;
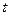– обозначение времени.
Параметр 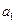определяет направление развития: если 
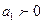, то уровни ряда равномерно возрастают в среднем за единицу времени на величину 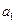, если 
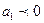, то происходит их равномерное снижение.
|
|
|
б) при постоянных темпах приростах делается вывод о равноускоренном или равнозамедленном типе развития, основная тенденция которого выражается уравнением параболы второго порядка: yt = a 0 + a 1 t + a 2 t 2.
Значение параметров 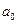и 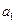идентично предыдущему уравнению.
Параметр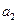 
характеризует изменение интенсивности развития в единицу времени. При 
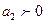происходит ускорение развития, при 
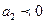– замедление развития.
Соответственно при параболической форме тренда возможны следующие варианты развития:
Ø если 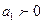; 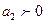– ускорение роста;
Ø если 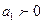; 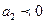– замедление роста;
Ø если 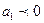; 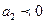– замедление снижения;
Ø если 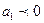; 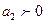– ускорение снижения.
в ) при стабильных цепных темпах роста делается вывод о развитии по экпоненте, основная тенденция которого выражается уравнением показательной функции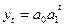 
, где 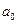– константа ряда, 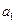–темп изменения в разах.
При 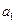>1 экспоненциальный тренд выражает тенденцию ускоренного и всё более ускоряющегося возрастания уровней, при 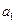<1 экспоненциальный тренд означает всё более замедляющегося снижения уровней динамического ряда.
г) при сокращении цепных абсолютных приростах в конечных уровнях ряда делается вывод о развитии с замедлением в конце периода, основная тенденция которого выражается уравнением логарифмической функции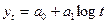 
.Логарифмическая форма тренда применяется для отображения тенденции замедляющегося роста уровней при отсутствии предельно возможного значения, например, роста спортивных достижений, производительности агрегата, продуктивности скота.
д) развитие с переменным ускорением (замедлением), основная тенденция которого выражается уравнением параболы третьего порядка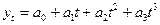 
. Параметр 
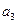отображает изменение ускорения (замедления);
|
|
|
е ) гиперболическая форма тренда yt = a 0 + a 1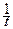 
, применим для отображения тенденции процессов, ограниченных предельным значением уровня;
ж) тренд в форме степенной функции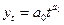 
, применим для отображения тенденции явлений с разной мерой пропорциональности изменений во времени;
з ) логистический тренд и др.
Ø аналитическое выравнивание динамического ряда: основная тенденция развития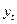 
рассчитывается как функция времени. В этом случае фактические (эмпирические) уровни заменяются теоретическими, вычисленными по соответствующему аналитическому уравнению.
При расчёте параметров трендовых моделей способом наименьших квадратов строятся и решаются системы нормальных уравнений:
для прямой линии для параболы 2-го порядка
.
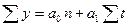
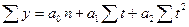
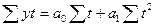
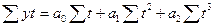
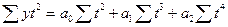Для упрощения решения систем применяется способ отсчёта от условного начала, при котором сумма показателей времени равна нулю.
При чётном числе уровней динамического ряда «t» обозначают следующим образом:
| и т.д. | -7 | -5 | -3 | -1 | и т.д. |
При нечётном числе уровней динамического ряда «t» обозначают следующим образом:
| и т.д. | -4 | -3 | -2 | -1 | и т.д. |
В этом случае система уравнений упрощается и приобретает вид для уравнения прямой линии: для уравнения параболы:
å y = a 0 n;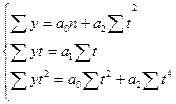 
å yt = a 1å t 2.
