2015-10-16
541
Таблица 11–Расчет данных для нахождения параметров уравнения параболы второго порядка
| Годы | Фактич. сумма на-логов, млн. руб. (y) | Обоз-начение периода (t) |
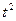
| y t |
y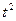
|
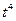
| Теоретич.
сумма
налогов,
млн. руб.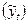 
| 
|
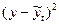
| -4 | -2304 | 592,5 | 272,25 | |||||
| -3 | -1923 | 629,2 | 139,24 | |||||
| -2 | -1358 | 653,1 | 670,81 | |||||
| -1 | -665 | 673,2 | 67,24 | |||||
| 686,5 | 812,25 | |||||||
| +1 | ||||||||
| +2 | 692,7 | 515,29 | ||||||
| +3 | 685,6 | 2246,76 | ||||||
| +4 | 671,7 | 388,09 | ||||||
| Итого | 5147,93 |
Поставим полученные суммы в систему уравнений:
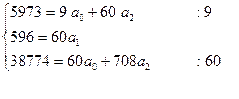
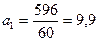
663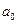,7= 
+ 6,7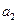 
646,2= 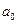+11,8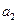
17,5= -5,1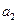
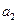= -3,4
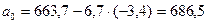
Таким образом, уравнение параболы второго порядка характеризующее тенденцию изменения налогов, уплаченных в местный бюджет хозяйствующими субъектами, имеет вид:
.
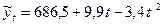При данных значения параметров (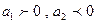
) основная тенденция характеризуется как замедленный рост.
Параметр «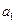
» характеризует средний ежегодный размер увеличения суммы налогов в анализируемый период – 9,9 млн. рублей; скорость замедление роста суммы налогов при нечетном числе уровней составляет 2 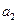- 6,8 млн. рублей.
Определим величину стандартной и относительной ошибки аппроксимации, используя данные последней графы таблиц 10 и 11:
;
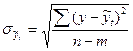для линейного тренда:
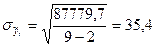млн. руб.;
.
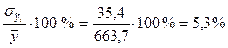для параболического тренда:
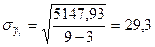млн. руб.
.
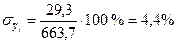Сравнив полученные значения ошибок для уравнений прямой и параболы второго порядка, можно сделать вывод о том, что парабола более точно описывает основную тенденцию ряда динамики суммы налогов, уплачиваемых хозяйствующих субъектов в местный бюджет.
