Линейная зависимость векторов

Выражение 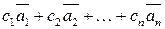называется линейной комбинацией векторов 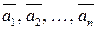с коэффициентами с₁, с₂,..., с_n.

Система векторов 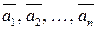называются линейно зависимой, если их линейная комбинация обращается в ноль 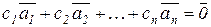при с₁, с₂,..., с_n, не равных нулю одновременно; и линейно независимой, если 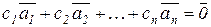только тогда, когда все коэффициенты с₁=с₂=...=с_n=0.

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Любые два неколлинеарных вектора линейно независимы. Любая система из трех векторов на плоскости линейно зависима.

Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Любые три некомпланарных вектора линейно независимы. Любая система из четырех векторов в пространстве линейно зависима.