Векторным произведением векторов  и
и  называется вектор
называется вектор 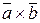 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) 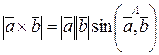 ; (2)
; (2)
2) 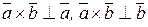 ;
;
3) тройка векторов  ,
,  ,
, 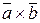 - правая (кратчайший поворот от вектора к вектору происходит против часовой стрелки).
- правая (кратчайший поворот от вектора к вектору происходит против часовой стрелки).
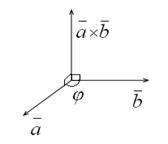
Алгебраические свойства векторного произведения:
1) 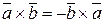 - свойство антикоммутативности;
- свойство антикоммутативности;
2) (a  )´
)´  = a (
= a (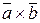 ) – свойство ассоциативности;
) – свойство ассоциативности;
3) 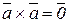 - векторное произведение вектора на себя равно нулю.
- векторное произведение вектора на себя равно нулю.
Геометрические свойства векторного произведения:
1) вектора  и
и  коллинеарны, если
коллинеарны, если 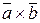 = 0;
= 0;
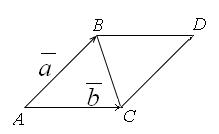
2) модуль векторного произведения |  ´
´  | равен площади S параллелограмма, построенного на приведенных к общему началу векторах
| равен площади S параллелограмма, построенного на приведенных к общему началу векторах  и
и  - геометрический смысл векторного произведения.
- геометрический смысл векторного произведения.
Векторное произведение в координатах векторов  (ха; уа; zа) и
(ха; уа; zа) и  (хb; уb; zb) есть вектор, вычисляемый по правилу:
(хb; уb; zb) есть вектор, вычисляемый по правилу: 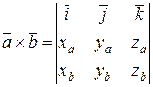 .
.
Из определения векторного произведения вытекают следующие формулы:
- синус угла между векторами 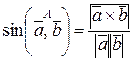 ;
;
- площадь треугольника, построенного на векторах  и
и  , равна 1/2|
, равна 1/2| 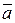 ´
´  |.
|.
 2015-10-16
2015-10-16 540
540








