Смешанным произведением упорядоченной тройки векторов 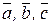 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 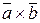 на вектор
на вектор 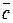 :
:
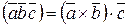 .
.
Алгебраические свойства смешанного произведения:
1) 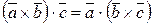 - смешанное произведение не изменяется от перегруппировки сомножителей;
- смешанное произведение не изменяется от перегруппировки сомножителей;
2) 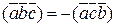 - смешанное произведение меняет знак на обратный при перестановке пары сомножителей;
- смешанное произведение меняет знак на обратный при перестановке пары сомножителей;
3) 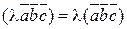 - при умножении вектора на число смешанное произведение умножается на это число.
- при умножении вектора на число смешанное произведение умножается на это число.
Геометрические свойства смешанного произведения:
1) три вектора 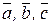 компланарны, если
компланарны, если 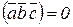 - условие компланарности трех векторов;
- условие компланарности трех векторов;
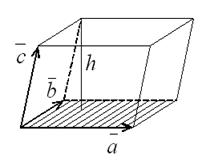
2) модуль смешанного произведения | 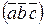 | некомпланарных векторов равен объему параллелепипеда, построенного на приведенных к общему началу векторах
| некомпланарных векторов равен объему параллелепипеда, построенного на приведенных к общему началу векторах  ,
,  и
и 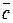 ;
;
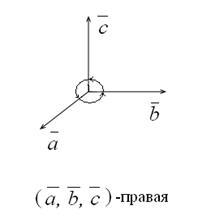
3) тройка векторов правая, если ( ,
,  ,
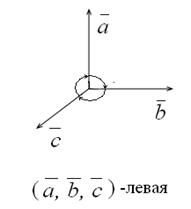
, 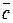 )>0; тройка левая, если (
)>0; тройка левая, если ( ,
,  ,
, 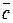 ) <0.
) <0.
Смешанное произведение в координатах трех векторов  ,
,  ,
, 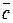 есть число, равное определителю, составленному из координат векторов:
есть число, равное определителю, составленному из координат векторов:
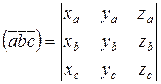 .
.
Из определения смешанного произведения векторов вытекают следующие формулы:
- объем тетраэдра 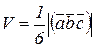 ;
;
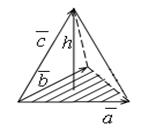
- высота тетраэдра (параллелепипеда) 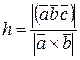 .
.
 2015-10-16
2015-10-16 464
464








