Неоклассическая модель роста Р. Солоу

После второй мировой войны теория роста стала развиватьс| ином по сравнению с довоенной депрессией контексте. 1950-е гс стали периодом устойчивого роста. В США бум был связан с KopJ

¹⁹ См ■ Классики кейнсианства. С. 124.

Ькой войной, в Западной Европе и в Японии — с американской по­мощью по плану Маршалла.

Так или иначе, стало ясно, что модель Харрода—Домара сильно преувеличивала неустойчивость западной экономики и недооцени-н та силы, ведущие к ее росту. С середины 1950-х годов начался но-и i.i и этап развития теории роста, который продолжался примерно до • редины 1970-х, когда на авансцену вышла теория цикла. Ключе-||мо роль на этом этапе сыграла модель роста Р. Солоу.

Американский экономист Роберт Солоу родился в 1924 г. в Нью-11орке, прошел курс наук и получил докторскую степень в Гарварде-i им университете. С 1950 г. преподает в Массачусетсском технологи-ком институте. Основной областью его интересов всегда была ма-юкономика, причем его подход заключался в построении моде-ц, оперирующих несколькими ключевыми показателями и пост-i-нных на микроэкономических принципах. Свои научные работы шоу в основном публиковал в виде журнальных статей и глав в кол-кгивных трудах. Наиболее известными его монографиями являют-■ Линейное программирование и экономический анализ» (совместно с Самуэльсоном и Р. Дорфманом (1958) и «Теорияроста:изложение» '69). За вклад в развитие теории экономического роста в 1987 г. >лоу была присуждена Нобелевская премия. Помимо научных ис-■цонаний и преподавания Солоу занимался практической деятель-i 1ъю в государственном секторе. Он входил в штат Совета эконо-ческих консультантов при президенте Дж. Кеннеди, позднее ра­кш в государственной комиссии, изучавшей проблемы доходов неления. В конце 1970-х годов Солоу в течение пяти лет был дирек-'|н>м Федерального резервного банка Бостона. Основы модели роста Солоу были изложены в его статье «Вклад в >рию экономического роста». Солоу пришел к выводу, что основ-н причиной неустойчивости экономики в модели Харрода—Дома-является фиксированная величина капиталоемкости (а), отража-мая жесткое соотношение между факторами производства — тру-м и капиталом (K/L). Неудивительно, что в этом случае один из ■ IX факторов часто остается «недогруженным». В соответствии же с кмципами неоклассической теории пропорции между капиталом i рудом должны быть переменными (именно в этом заключается i'классический характер теории роста Солоу)²¹. Они определяются

'" Solow R. A Contribution to the Theory of Economic Growth // Quarterly ii "irnal of Economics. 1956. February.

^л Хотя, например, в модели общего равновесия Вальраса, ставшей од­ним и j истоков неоклассической теории, предполагалась неизменная про­порция между трудом и капиталом. Дай сам Солоу в своих взглядах намак-i"p жономические проблемы был скорее кейнсианцем, а не неоклассиком.

минимизирующими издержки производителями в зависимости от щ на эти факторы производства. Поэтому вместо фиксированного. Солоу включил в свою модель линейно-однородную производстве^ ную функцию:

Y= F{K, L).

Разделив все члены на L и обозначив доход на одного работай! (У/L) через у, а капиталоинтенсиЕНОсть K/L через к, получим:

y=LF(k,\) = L№.

Как и в модели Харрода—Домара, предполагается, что населений

растет неизменным темпом и, а инвестиции составляют постояннун

долю дохода, определяемую нормой сбережения s:

I=sY. Темп прироста £ тогда можно записать как

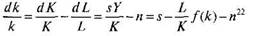
или

dk' = sf(k)-nk.

Это так называемое «фундаментальное уравнение» Солоу слои.1 ми выражается так: прирост капиталовооруженности одного раб<" ннка — это то, что осталось от удельных инвестиций (сбережени после того как удалось обеспечить капитальными благами всех полнительных работников.

Если sf(k) = пк, то капиталовооруженность остается прежЕ (elk = 0), т.е. экономика растет без каких-либо структурных измене] в соотношении между факторами. Это и есть сбалансированный pt

В модели Солоу в противоположность модели Харрода—Дом. траектория сбалансированного роста является устойчивой. Со) показывает эт.о с помощью следующего графика (рис. 1).

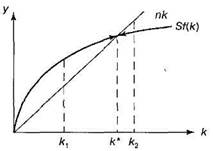
Рис. 1

²² dk, dKv\ dL обозначают дифференциальные приросты соответствую^ щих переменных. См. сноску 18 к этой главе.

Прямая пк на этом графике показывает, сколько каждый работ-

; должен сберегать и инвестировать из своего дохода, чтобы обес-(шъ будущих работников (в том числе своих собственных детей) 1игальными благами.

Кривая sf(k) демонстрирует, каковы его фактические сбережения

Цшисимости от достигнутого уровня капиталовооруженности.

ростом капиталовооруженности к темп роста инвестиций/сбереже-

\, естественно, падает. Вертикальное расстояние между кривой и

1мой обозначает в соответствии с фундаментальным уравнением

поу дифференциальное изменение показателя капиталовооружен-

C'iii dk. В точке к* оно равно нулю и наблюдается сбалансирован-

й рост. Во всех точках левее к* (например, к_{) капиталовооружен-

;i i. будет расти, а во всех точках правее к* (например, к₂) падать,

•но экономика постоянно сдвигается в сторону /с* и траектория [лансированного роста является устойчивой.

И модели Солоу норма сбережений s имеет значение только до Кода экономики на траекторию устойчивого развития: чем больше кичина s, тем выше график sk и соответственно уровень к*. Но как 1I.K0 рост стал сбалансированным, его дальнейший темп зависит (|1.ко от роста населения и технологического прогресса.

«Золотое правило». Из модели Солоу следовало, что чем больше рмп сбережений, тем выше капиталовооруженность работника в 1 оннии сбалансированного роста и, следовательно, тем выше темп таксированного роста. Но сам по себе рост не является самоце-). Поэтому следующим шагом, логически вытекающим из моде-j было определение условий оптимального для общества экономи­кою роста. Этот шаг одновременно и независимо друг от друга Шали несколько экономистов (Т. Суон, Дж. Мид, М. Алле, Дж, Ро-чсон, К. фон Вайцзеккер и др.) в самом начале 1960-х годов. Но)пым опубликовал ответ на данный вопрос американский эконо-Ст Эдмунд Фелпс. Ему же принадлежит и термин «золотое прави-нпкопления капитала», вошедший с тех пор в широкое употребле-6. Фслпс задался вопросом, какой величины капитал захочет иметь цсство, находящееся натраектории сбалансированного роста. Если I будет достаточно большим, это гарантирует высокий уровень про-родсгва, но все большая его часть пойдет не на потребление, а на копление — общество не сможет насладиться плодами роста. Если | объем капитала будет слишком малым, то потреблять можно бу-¹ почти все, что произведено, но произведено то будет совсем не-|oio! Где-то посредине между этими двумя крайностями, очевид-i находится оптимальная для общества точка, в которой объем по-

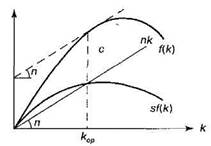требления общества является максимальным. Это можно следующим образом показать на графике (рис. 2).

Рис.2

К графику на рис.1 мы добавим кривую выпуска или дохода на душу населения у =f(k). Тогда максимизироваться будет вертикаль ное расстояние между кривой дохода на душу населения и инвести­ций надушу населения:/(£) — sf(k) =/(£) - пк (в случае сбалансиро­ванного роста). Это расстояние является максимальным в точке, где угол наклона касательной к кривой/(£) равен углу наклона прямой пк, т.е. п. Это задает оптимальный уровень капиталоинтенсивности к_вГ Остается выбрать такую норму потребления/накопления, чтобы кри­вая sf(k) пересекала луч пк в точке, соответствующей к_о.

Если мы далее (вместе с перечисленными выше авторами, но за исключением Фелпса) предположим, что в нашей экономике суще­ствует совершенная конкуренция на рынках факторов производства и, следовательно, действует теория предельной производительности (см. гл. 17), то угол наклона/(&), т.е. предельная производительность капитала, должен быть равен ставке процента г. В этом случае «золо­тое правило» можно сформулировать так: ставка процента должна быть равна темпу роста населения, а значит (при сбалансированном росте), и всей экономики:

г = п.

Следовательно, в экономике, испытывающей бурный рост, став­ки процента должны при прочих равных условиях быть высокими.

Применимость «золотого правила» на практике оказалась весьма ограниченной ввиду достаточно сильных исходных предпосылок, но оно позволило сформулировать выводы, относящиеся к реальному экономическому росту.

Модель Солоу и «золотое правило» оказались достаточно просты­ми и чрезвычайно удобными в употреблении аналитическими ору

Виями. С их помощью оказалось возможно исследовать влияние на (экономический рост различных модификаций производственной (функции, технического прогресса, изменения нормы сбережений и [Налогообложения и т.д. Усилиями самого Солоу, Д.Мида и других эко­номистов модель Солоу была дезагрегирована: отдельно учитывалось [Производство потребительских и инвестиционных благ. Были созда-1ны также модели, учитывающие «позраст» капитальных благ, посколь­ку разные их поколения обладают разной производительностью

(vintage models). Работы Джеймса Тобина ввели в теорию роста де­нежную массу (точнее, государственные обязательства, которыми [люди владеют наряду с капиталом).