Интегральное исчисление функции

11) Вычислить неопределенные и определенные интегралы

Решение:

a) = =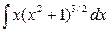

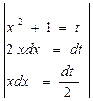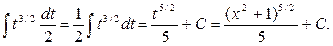
b) .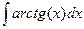

Интегирируется по частям: пусть 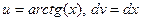; тогда , 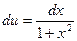. Следовательно, .

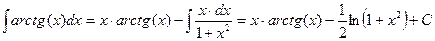c)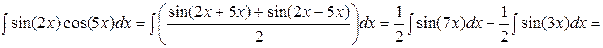

.

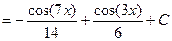d) = = =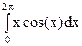

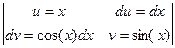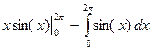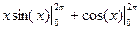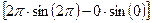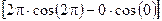= + =0.

e)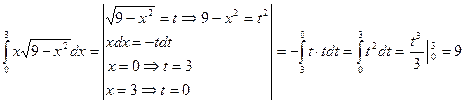

12)Построить схематический чертёж и найти площадь фигуры ограниченной линиями: а) , , ;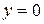

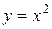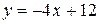Решение:

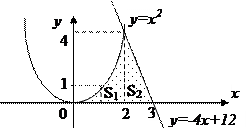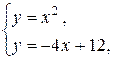
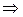
а) I способ. Найдем точки пересечения графиков 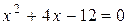. Решая квадратное уравнение получаем

, .

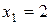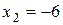Рис.6

Из рис. 6 видно, что площадь равна сумме площадей криволинейных трапеций.

.

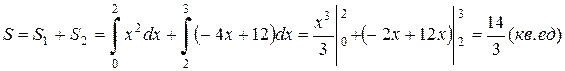II способ. Площадь можно найти через двойной интеграл.

.

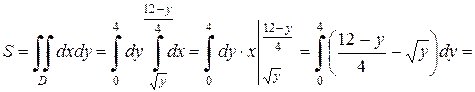
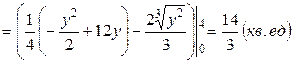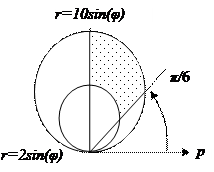б) , , , .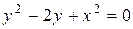

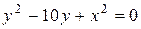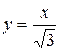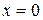В данных уравнениях встречается выражение 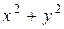, значит, для вычисления площади криволинейной трапеции можно перейти к полярным координатам.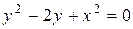

, , .

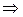
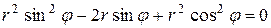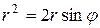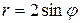Рис. 7

Аналогично .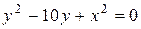

, , .

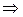
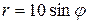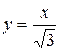
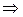
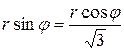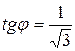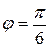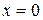
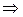
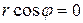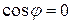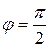, , . Область интегрирования изображена на рис.7.

.

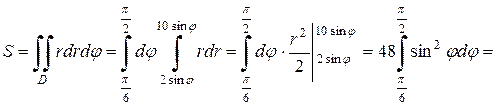
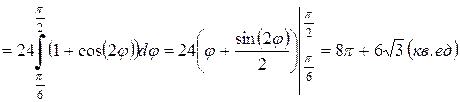СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Агишева Д. К. Матрицы и их приложение к решению систем линейных уравнений: Учебное пособие/ Д. К. Агишева, С. А. Зотова, В. Б. Светличная. - Волгоград, РПК «Политехник», 2001. – 63с.

2. Александрова Л. А, Александрова В. А, Зотова С. А., Светличная В. Б., Матвеева Т. А., Короткова Н. Н. Математика. I часть: Учебное пособие (для студентов заочной формы обучения) / – Волгоград, РПК «Политехник», 2003. – 84с.

3. Письменный Д. Т. Конспект лекций по высшей математике. 1 часть. – М.: Рольф, 2000. – 288 с., с илл.

4. Лунгу К. Н., Письменный Д. Т., Федин С. Н., Шевченко Ю. А. Сборник задач по высшей математике. 1 курс. – М.: Рольф, 2001. – 576 с., с илл.

5. Зотова С. А., Светличная В. Б., Матвеева Т. А.. Практическое руководство по аналитической геометрии: Учебное пособие / – Волгоград, РПК «Политехник», 2003. – 41с.

6. Кузнецов Л. А. Сборник заданий по высшей математике. Типовые расчеты – М.: Высшая школа, 1983.

7. Клетеник Д. В. Сборник задач по аналитической геометрии: Учебное пособие для втузов – СПб: «Специальная Литература», 1998.–200 с.: илл.

8. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1981.–720с.: илл.

9. Выгодский М. Я. Справочник по высшей математике. –М.: Гостехтеоргиздат, 1973.