1)Даны матрицы: 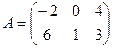 ,
, 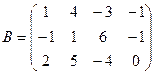 ,
, 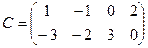 .
.
Найти 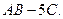
Решение:
Матрица А имеет размерность 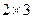 , матрица В размерность
, матрица В размерность 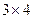 . Т.к. число столбцов первой матрицы равно числу строк второй матрицы, то данные матрицы можно перемножить. В результате получится некоторая матрица D, имеющая размерность
. Т.к. число столбцов первой матрицы равно числу строк второй матрицы, то данные матрицы можно перемножить. В результате получится некоторая матрица D, имеющая размерность 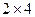 .
.
Найдем элементы матрицы D:
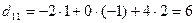 ;
; 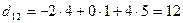 ;
; 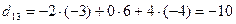 ;
; 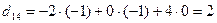 ;
;
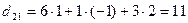 ;
; 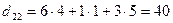 ;
; 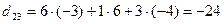 ;
; 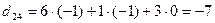 .
.
Тогда 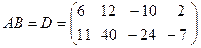 .
.
По правилу умножения матрицы на число 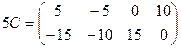
Найдём 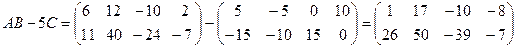 .
.
2) Решить систему методом Крамера: 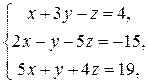
Решение:
Вычислим основной определитель, раскладывая его по 1-ой строке через алгебраические дополнения:
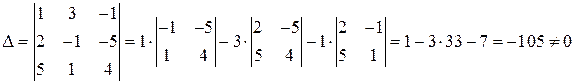 ,
,
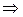 система имеет единственное решение.
система имеет единственное решение.
Вычислим вспомогательные определители системы:
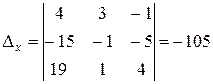 ;
; 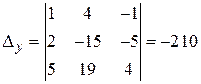 ;
; 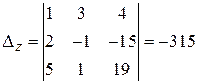 .
.
Отсюда по формулам Крамера находим:
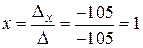 ,
, 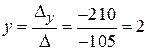 ,
, 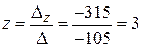 .
.
Сделаем проверку подстановкой найденных значений в исходную систему:
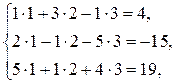 - верно.
- верно.
3) Решить систему методом Жордана – Гаусса:
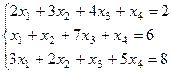
Решение:
Рассмотрим расширенную матрицу системы: 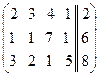 . Приведём её к верхнетреугольному виду.
. Приведём её к верхнетреугольному виду.
Поменяем местами 1-ю и 2-ю строки: 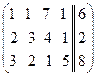 . Из 2-ой стоки вычтем 1-ю строку, умноженную на 2, из 3-ей стоки вычтем 1-ю строку, умноженную на 3:
. Из 2-ой стоки вычтем 1-ю строку, умноженную на 2, из 3-ей стоки вычтем 1-ю строку, умноженную на 3: 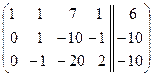 . К 3-ей строке прибавим 2-ю строку:
. К 3-ей строке прибавим 2-ю строку: 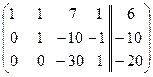 . Третью строку разделим на (-30):
. Третью строку разделим на (-30): 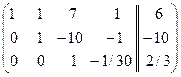 . Переменные
. Переменные 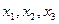 являются базисными, а переменная
являются базисными, а переменная 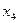 является свободной. Заменим исходную систему системой, полученной путём преобразования матрицы и выразим базисные переменные через свободные:
является свободной. Заменим исходную систему системой, полученной путём преобразования матрицы и выразим базисные переменные через свободные: 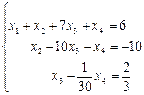 . Выразим из 3-го уравнения
. Выразим из 3-го уравнения 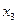 и подставим его значение во второе уравнение, затем из 2-го уравнения выразим
и подставим его значение во второе уравнение, затем из 2-го уравнения выразим 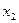 и подставим в 1-е уравнение. Тогда система примет вид:
и подставим в 1-е уравнение. Тогда система примет вид: 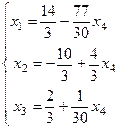 . Свободная переменная
. Свободная переменная 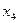 может принимать любые значения. Зададим
может принимать любые значения. Зададим 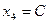 , где С - произвольная константа. Тогда решение системы может быть представлено в виде матрицы-столбца:
, где С - произвольная константа. Тогда решение системы может быть представлено в виде матрицы-столбца: 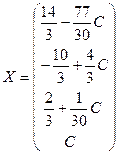 .
.
4) Даны координаты вершин треугольника, A (3, 5), B (-7, 12), C (2, -6). Найти:
a) длину стороны AB;
b) общие уравнения сторон AB и BC;
c) величину угла B;
d)длину и уравнение высоты, опущенной из вершины 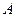 ;
;
e) площадь треугольника 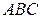 .
.
Решение:
a)Найдём длину стороны AB, как длину вектора 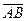 :
: 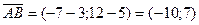 .
. 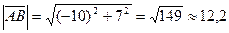 .
.
b)Найдём уравнения сторон AB и BC по формуле уравнения прямой, проходящей через две точки.
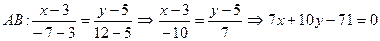 - общее уравнение прямой АВ.
- общее уравнение прямой АВ.
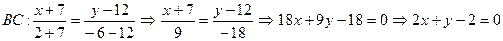 - общее уравнение прямой ВС.
- общее уравнение прямой ВС.
 c) Угол В – есть угол между прямыми AB и BC. Угол между прямыми может быть найден, как угол между их нормальными векторами.
c) Угол В – есть угол между прямыми AB и BC. Угол между прямыми может быть найден, как угол между их нормальными векторами. 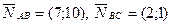 .
. 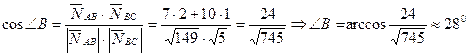 .
.
d) Опустим высоту из точки А на сторону ВС. Пусть точка D – есть основание этой высоты. Прямая AD перпендикулярна прямой ВС. Следовательно, вектор нормали прямой ВС является направляющим вектором для прямой AD. 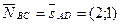 . Воспользуемся каноническим уравнением прямой.
. Воспользуемся каноническим уравнением прямой. 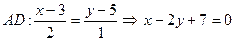 - общее уравнение высоты AD.
- общее уравнение высоты AD.
Найдём длину высоты AD, как расстояния от точки А до прямой ВС.
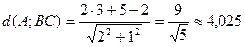 .
.
e)Найдём площадь треугольника 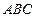 как половину произведения длины основания треугольника на его высоту.
как половину произведения длины основания треугольника на его высоту.
Пусть ВС – основание  , AD – его высота.
, AD – его высота.
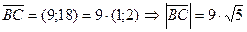 ;
; 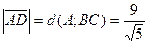 .
.
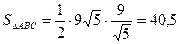 .
.
5) Даны четыре точки A (3;-2;1), B (1;2;4), C (-5;4;6), M (2;3;-1). Найти:
a)уравнение плоскости a, проходящей через три точки A, B, C;
b)каноническое уравнения прямой AB;
c)уравнение и длину высоты, опущенной из вершины М на грань 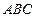 ;
;
d) объем пирамиды АВСМ.
Решение:
a)Воспользуемся уравнением плоскости, проходящей через три точки: 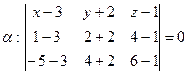
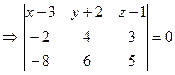
Разложим определитель по элементам первой строки:
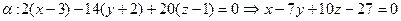 - общее уравнение плоскости α.
- общее уравнение плоскости α.
b) Воспользуемся уравнением прямой, проходящей через две точки:
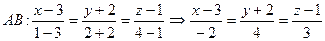 - каноническое уравнение прямой АВ.
- каноническое уравнение прямой АВ.
c) Обозначим высоту, опущенной из вершины М на грань 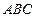 через l. Т.к
через l. Т.к 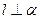 , то
, то 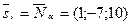 . Составим каноническое уравнение прямой l:
. Составим каноническое уравнение прямой l: 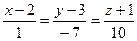 .
.
Найдём длину высоты как расстояние от точки М до плоскости α: 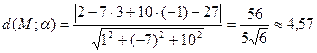 .
.
d)Объём пирамиды равен 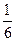 объёма параллелепипеда, построенного на трёх векторах и может быть вычислен через смешанное произведение этих векторов:
объёма параллелепипеда, построенного на трёх векторах и может быть вычислен через смешанное произведение этих векторов: 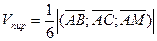 .
.
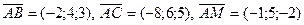
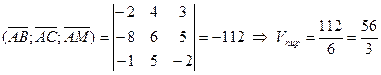 .
.
 2015-10-16
2015-10-16 1005
1005








