6)Вычислить пределы, не пользуясь правилом Лопиталя.
Решение:
a) 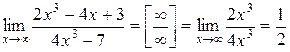 . Предел отношения многочленов и иррациональностей при
. Предел отношения многочленов и иррациональностей при 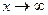 равен пределу отношения старших по степени слагаемых.
равен пределу отношения старших по степени слагаемых.
b) 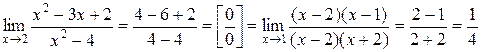 .
.
с) 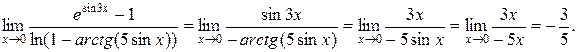
d)Воспользуемся обобщённой формулой второго замечательного предела:
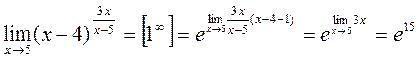 .
.
7) Найти производные первого порядка для следующих функций:
a) 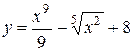 b)
b) 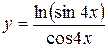
Решение:
a) 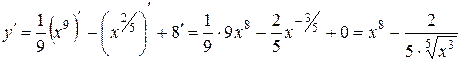 .
.
b) Воспользуемся формулой для нахождения производной частного:
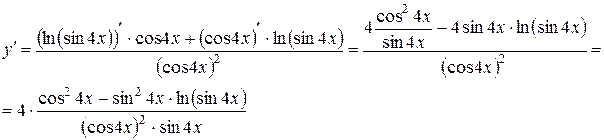
8) Дана функция 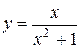 . Найти уравнения касательной и нормали к графику функции в точке x0=-2.
. Найти уравнения касательной и нормали к графику функции в точке x0=-2.
Решение:
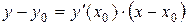 - уравнение касательной.
- уравнение касательной.
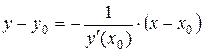 - уравнение нормали.
- уравнение нормали.
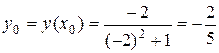 ;
;
По формуле для нахождения производной частного:
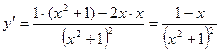 ;
; 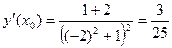 .
.
Тогда уравнение касательной: 
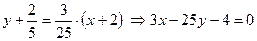 ;
;
Уравнение нормали: 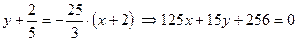 .
.
9) Дана функция 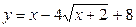 . Найти наибольшее и наименьшее значения функции на отрезке
. Найти наибольшее и наименьшее значения функции на отрезке 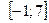 .
.
Решение:
Вычислим производную 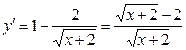 .
.
Найдём критические точки:
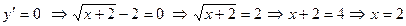
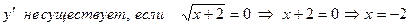
Точка 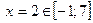 ,
, 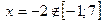 .
.
Найдём 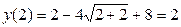 .
.
Найдём значения функции на концах отрезка:
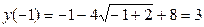 ;
; 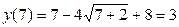 .
.
Наибольшее значение на данном отрезке достигается функцией в двух точках – на концах отрезка: 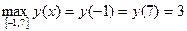 .
.
Наименьшее значение на данном отрезке достигается функцией во внутренней точке отрезка: 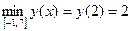 .
.
10) Даны функция 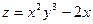 , точка A(2;-1) и вектор
, точка A(2;-1) и вектор 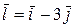 . Требуется найти
. Требуется найти 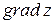 и производную в точке A по направлению вектора
и производную в точке A по направлению вектора 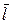 .
.
Решение:
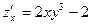 ;
; 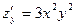 ;
; 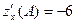 ;
; 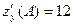
Следовательно 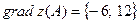 .
.
Найдём направляющие косинусы вектора 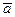 :
:
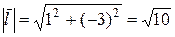 ;
; 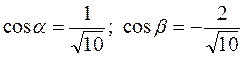 .
.
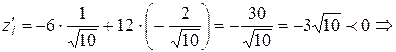 данная функция убывает в направлении вектора
данная функция убывает в направлении вектора 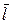 .
.
 2015-10-16
2015-10-16 490
490








