ЛАБОРАТОРНАЯ РАБОТА №2
Тема работы: Точечные и интервальные (доверительные) оценки параметров нормально распределенной случайной величины.
Цель работы: Научиться определять точечные и интервальные оценки математического ожидания и дисперсии нормально распределенных случайных величин. Уяснить вопрос о зависимости интервальных оценок от объема выборки и уровня доверительной вероятности.
Задание: По заданной совокупности результатов эксперимента 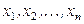 построить точечную и двустороннюю интервальную оценку для истинного значения измеряемой величины (при известной и неизвестной погрешности измерений); построить точечную и двустороннюю интервальную оценку для погрешности измерений (при известном и неизвестном значении измеряемой величины).
построить точечную и двустороннюю интервальную оценку для истинного значения измеряемой величины (при известной и неизвестной погрешности измерений); построить точечную и двустороннюю интервальную оценку для погрешности измерений (при известном и неизвестном значении измеряемой величины).
Теоретическая часть
Доверительный интервал для истинного значения измеряемой величины.
Допустим, что все 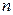 измерений
измерений 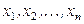 величины
величины 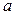 взаимно независимы и произведены с одинаковой точностью
взаимно независимы и произведены с одинаковой точностью 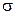 (которая предполагается известной, например, по результатам предыдущих измерений), и случайные погрешности измерений подчиняются нормальному распределению. Тогда интервал
(которая предполагается известной, например, по результатам предыдущих измерений), и случайные погрешности измерений подчиняются нормальному распределению. Тогда интервал
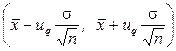 (1)
(1)
со случайными границами есть (двусторонний) доверительный интервал (или интервальная оценка) величины 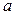 с мерой надежности
с мерой надежности 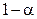 , т. е.
, т. е.
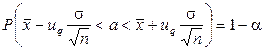 .
.
Здесь 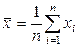 - точечная оценка измеряемой величины,
- точечная оценка измеряемой величины, 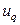 - квантиль стандартного нормального распределения уровня
- квантиль стандартного нормального распределения уровня 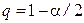 , определяемый из решения уравнения
, определяемый из решения уравнения
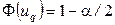 ,
,
где 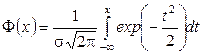 - функция стандартного нормального распределения,
- функция стандартного нормального распределения, 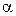 - уровень значимости. Число
- уровень значимости. Число 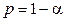 называется доверительной вероятностью или уровнем (мерой) надежности оценки.
называется доверительной вероятностью или уровнем (мерой) надежности оценки.
Если точность измерений (т.е. среднеквадратичная ошибка 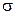 ) заранее не известна, то сначала вычисляется ее оценка (
) заранее не известна, то сначала вычисляется ее оценка (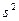 – несмещенная оценка дисперсии,
– несмещенная оценка дисперсии, 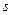 оценка среднеквадратичной ошибки)
оценка среднеквадратичной ошибки)
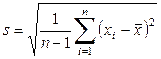 ,
,
а затем строится доверительный интервал
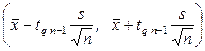 , (2)
, (2)
где 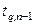 - квантиль уровня
- квантиль уровня 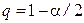 распределения Стьюдента с
распределения Стьюдента с 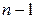 степенями свободы, определяемый как корень уравнения
степенями свободы, определяемый как корень уравнения
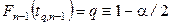 ;
;
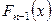 - функция распределения Стьюдента с
- функция распределения Стьюдента с 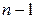 степенями свободы. Если для оценки среднеквадратичной ошибки используется смещенная оценка дисперсии
степенями свободы. Если для оценки среднеквадратичной ошибки используется смещенная оценка дисперсии 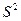 , т.е.
, т.е.
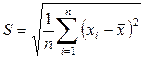 ,
,
то доверительный интервал (2) для параметра 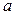 записывается в виде
записывается в виде
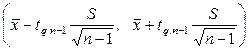 .
.
 2015-10-16
2015-10-16 773
773







