Элементы дифференциального исчисления

Производная функции одной переменной

Пусть задана функция 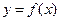. Возьмем произвольную точку 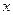и найдем значение 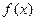(рис.1). Дадим независимой переменной 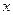приращение 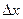и найдем .

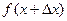Составим разность 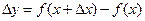, называемую приращением функции 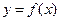в точке .

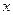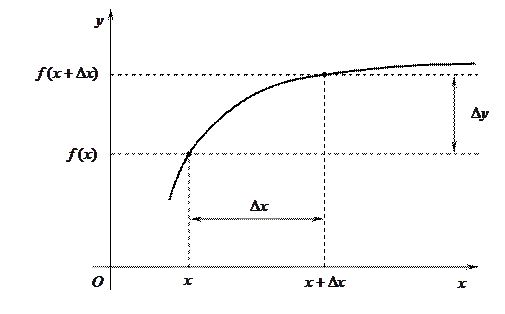Рис.1. График функции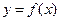

Производная функции одной переменной 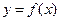в точке х представляет собой предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю. При конкретном значении х производная функции 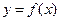представляет собой определенное число, зависящее от самой функции и от точки х. Отсюда следует, что сама производная 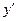в области определения функции 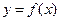также является некоторой функцией той же независимой переменной х.

Нахождение этой функции называется дифференцированием функции 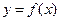и представляет собой одну из основных задач дифференциального исчисления.

Геометрический смысл производной.

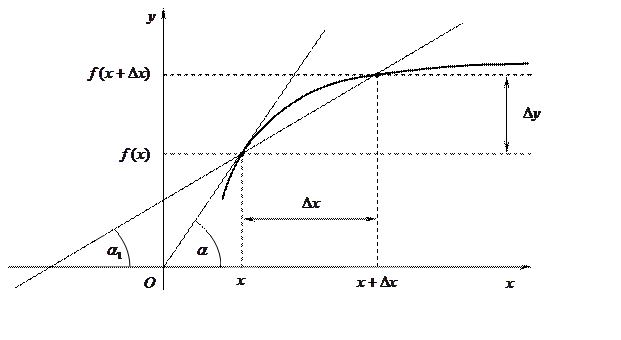
Рис.2. Геометрический смысл производной

Произведение в виде

.

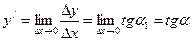где 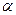- угол наклона к оси 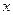касательной к графику функции в точке с координатами 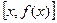. В этом состоит геометрический смысл производной.

Значение производной при данном значении 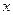равно тангенсу угла, образованного касательной к графику функции в точке с соответствующим значением х с положительным направлением оси О х.

Производная 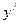в каждой точке х характеризует скорость изменения функции в данной точке. Чем больше абсолютная величина производной, тем быстрее изменяются значения функции, проходя через эту точку.

Правила вычисления производных простейших элементарных функций

Таблица производных простейших элементарных функций

1. , .

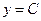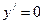2. , .

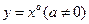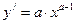3. , , , .

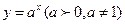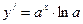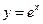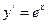4. , , , .

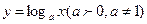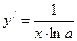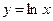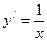5. , .

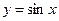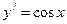6. , .

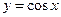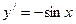7. , .

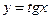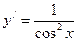8. , .

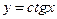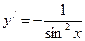9. , .

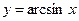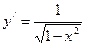10. , .

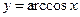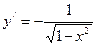11. , .

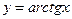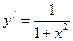12. , .

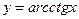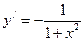Правила нахождения производной в алгебраических действиях.

Пусть 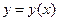, , 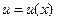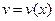- функции независимой переменой 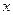, 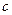- постоянная величина. Тогда:

1. Постоянный множитель можно выносить за знак производной. Если

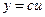, то .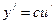

2. Производная алгебраической суммы равна алгебраической сумме производных:

, .

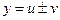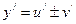3. Производная произведения равна сумме произведений производной первого сомножителя на производную второго, т.е. если

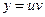, то .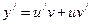

4. Производная частного равна разности произведений производной числителя на знаменатель и числителя на производную знаменателя, деленной на квадрат знаменателя. Если

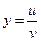, то .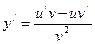

5. Производная сложной функции.

Пусть 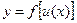. Тогда производная 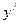равна произведению производной функции 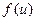, где функция 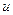считается независимой переменной, на производную функцию 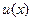, т.е.

.

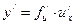Дифференциал

Если приращение 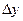функции 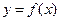в точке х можно представить в виде

,

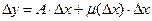Где А – число, а функция 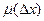такова, что

,

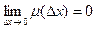то величина 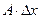называется дифференциалом функции 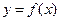в точке х и обозначается 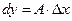, а сама функция 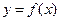называется дифференцируемой в точке .

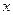Выражение для дифференциала

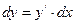
Производная равна отношению дифференциалов функции и независимой переменной

.

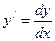Геометрический смысл дифференциала

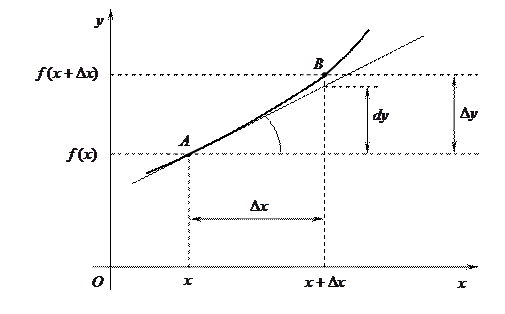
Рис.3. Геометрический смысл дифференциала

Из рисунка очевидно, что касательная к графику функции 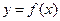отсекает от приращения функции 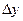отрезок, длинна которого равна

.

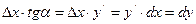То есть длинна этого отрезка равна дифференциалу функции.

Дифференциал сложной функции равен произведению производной функции на дифференциал переменной по которой находится производная.

Понятие дифференциала можно применить для приближенного вычисления значений функций.

Тогда приближенно запишем

.

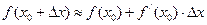Теоремы дифференциального исчисления

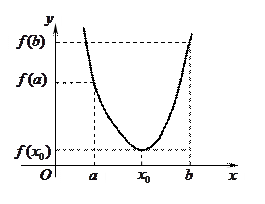
Теорема Ферма. Если дифференцируемая на промежутке 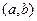функция 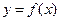достигает наибольшего или наименьшего значения в точке 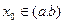, то производная функция в этой точке равна нулю, т.е. .

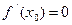Теорема Ролля. Пусть функция 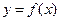удовлетворяет следующим условиям:

1. непрерывна на отрезке ;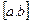

2. дифференцируема на интервале ;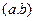

3. на концах отрезка 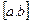принимает равные значения, т.е. .

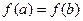Тогда внутри отрезка существует хотя бы одна точка 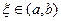, в которой производная равна нулю 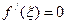(на рисунке таких точек две).

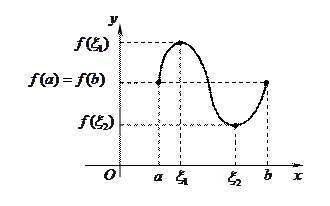
Геометрически это означает, что при выполнении условий теоремы Ролля найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.

Обобщением теоремы Ролля является теорема Лагранжа.

Пусть функция 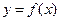является непрерывной на отрезке 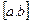и дифференцируемой на интервале 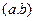. Тогда внутри отрезка существует по крайней мере, одна точка 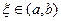, в которой производная функции равна нулю

.

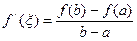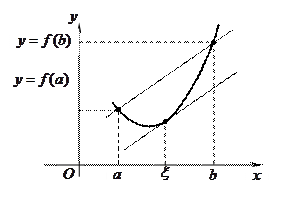
Геометрическая теорема означает, что найдется хотя бы одна точка 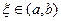, в которой касательная к графику функция 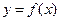и хорда АВ параллельны.

Используя геометрический смысл производной можно легко составить уравнения касательной и нормали к графику функции 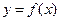в точке А с координатами 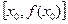. Действительно, формула 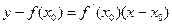определяет касательную, а формула

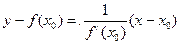
- нормаль к графику функции 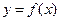в точке А.

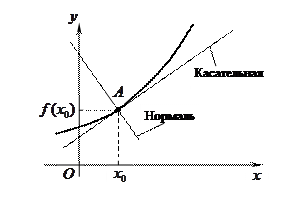
Производные и дифференциалы высших порядков

Пусть функция 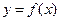определена и имеет производную в некоторой области определения Х. Как показано ранее, производная 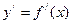также является функцией той же независимой переменной .

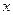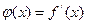
и тоже может иметь производную 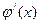в области определения Х.

Эта производная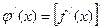

называется второй производной (или производной второго порядка) функции 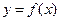и обозначается 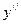или .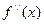

Дифференциалом второго порядка (вторым дифференциалом) функции 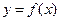называется дифференциал от первого дифференциала

.

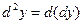Правило Лопиталя раскрытия неопределенностей

Для раскрытия неопределенностей вида 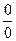или 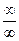используется правило Лопиталя. То есть это правило применяется, когда нужно найти предел

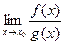, ес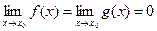ли или .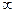

Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных конечному или бесконечному), если последний существует.

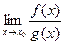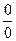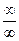Другими словами, если - неопределенность вида или , то

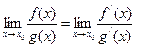
Замечания.

1. Правило Лопиталя неприменимо, когда пределы числителя и знаменателя одновременно не равны нулю или бесконечности.

2. При использовании правила Лопиталя находится предел отношения производных числителя и знаменателя, т.е.

,

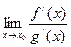а не предел производной отношения

.

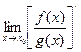5. Рекомендуемое содержание отчета (для студента).

1. Название лабораторной работы.

2. Цель и задачи исследований.

3. Электронно-вычислительные средства для расчетов.

4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).

5. Выводы.

6. Анализ и защита лабораторной работы производится по результатам представленного студенческой группой отчета (перечень сделанного, рекомендации, представленные основные элементарные функции (формула, основные свойства, график), ответы на рассмотренные в процессе выполнения контрольные вопросы).

Преподаватель оценивает знание каждого студента.

Литература