(2 часа)
Цель: овладеть математическими знаниями и навыками исследования функций и построения графиков функций для использования их в задачах практического содержания.
На лабораторном занятии формируются
знания:
- о монотонности функции,
- о точки минимума (максимума),
- о необходимом условии экстремума функции,
- о первом и втором достаточных условиях экстремума,
- о точке перегиба,
- о достаточном условии выпуклости (вогнутости) графика функции;
умения:
-нахождения интервалов монотонности и экстремумов функции,
- выполнять действий при нахождении интервалов выпуклости и вогнутости, а также точек перегиба графика функции;
навыки:
- применения исследования функций и построения графика функции в задачах практического содержания.
Материально-техническое оборудование:
компьютерный класс.
ПЛАН ЗАНЯТИЯ
1. Инструктаж по ТБ.
2.Проверка знаний студентов — их теоретической готовности к выполнению заданий.
3. Общее описание задания.
4. Выполнение заданий.
5. Оформление отчета о лабораторной работе.
6. Анализ
Глоссарий
Выучите определения следующих терминов:
монотонность функции, признак монотонности функции, основные способы задания функции, точки минимума (максимума), критические точки, стационарные точки, достаточное условие возрастания и убывания функции на интервале, необходимое условие экстремума функции, достаточное условие выпуклости (вогнутости) графика функции на интервале, точка перегиба, необходимое и достаточное условия точки перегиба, асимптота графика функции, исследование и построением графика функции.
ХОД ЗАНЯТИЯ
1. Инструктаж по ТБ.
2. На лабораторном занятии используется фронтальная и индивидуальная формы работы.
Контрольные вопросы
1. Что называется интервалом монотонности функции? ((ОК-1, ОК-20, ОК-22, ПК-31)
2.Сформулируйте достаточное условие возрастания (убывания) функции на интервале. (ОК-1, ОК-20, ОК-22, ПК-31)
3. Что называется точкой и значением максимума (минимума) функции? Какое общее название имеют максимум и минимум? (ОК-1, ОК-20, ОК-22, ПК-31)
4. Сформулируйте необходимое условие экстремума функции. (ОК-1, ОК-20, ОК-22, ПК-31)
5. Как называются точки, в которых выполнено необходимое условие экстремума функции? (ОК-1, ОК-20, ОК-22, ПК-31)
6. Сформулируйте первое и второе достаточные условия экстремума. (ОК-1, ОК-20, ОК-22, ПК-31)
7. Изложите порядок действий при нахождении интервалов монотонности и экстремумов функции. (ОК-1, ОК-20, ОК-22, ПК-31)
8.Какой график функции является выпуклым (выпуклым вверх), а какой вогнутым (выпуклым вниз) на интервале? (ОК-1, ОК-20, ОК-22, ПК-31)
9. Какая точка называется точкой перегиба графика? (ОК-1, ОК-20, ОК-22, ПК-31)
10. Сформулируйте достаточное условие выпуклости (вогнутости) графика функции на интервале. (ОК-1, ОК-20, ОК-22, ПК-31)
11. Сформулируйте необходимое и достаточное условия точки перегиба. (ОК-1, ОК-20, ОК-22, ПК-31)
11.Изложите порядок действий при нахождении интервалов выпуклости и вогнутости, а также точек перегиба графика функции. (ОК-1, ОК-20, ОК-22, ПК-31)
3. Необходимо выполнить:
- представленные общие исходные задания;
- представленные индивидуальные задания для студентов, работающих в более быстром темпе (можно выполнить в качестве Д/з);
- оформление отчета о лабораторной работе;
- защита лабораторной работы производится в индивидуальном порядке.
4. Задания
Общие:
№1. Найти интервалы монотонности и экстремумы функций:
1) y =х3+3х2-9х+12. (ОК-1, ОК-20, ОК-22, ПК-31)
№2.Найти интервалы выпуклости и вогнутости, а также точки перегиба графика функции у = х4 +2х3—12х2—5х+2. (ОК-1, ОК-20, ОК-22, ПК-31)
№3. Произвести полное исследование функции и построить график функцииу = 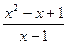 (ОК-1, ОК-20, ОК-22, ПК-31)
(ОК-1, ОК-20, ОК-22, ПК-31)
Индивидуальные: (ОК-1, ОК-20, ОК-22, ПК-31)
Задание: Произвести полное исследование функции и построить график функции.
Вариант 1. Вариант 2.
у = 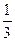 х3—
х3— 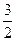 х2—4х + 10; у = -
х2—4х + 10; у = - 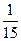 х3 +
х3 + 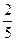 х2 +
х2 + 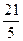 х — 1;
х — 1;
Вариант 3. Вариант 4.
у = 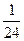 х3 +
х3 + 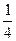 х2 —
х2 — 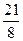 х — 1; у =
х — 1; у = 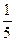 х3—
х3— 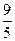 х2 +3х + 3;
х2 +3х + 3;
Вариант 5. Вариант 6.
у = - 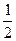 х3 + 6х — 1; у =
х3 + 6х — 1; у = 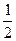 х3 + 3х2—7;
х3 + 3х2—7;
Вариант 7. Вариант 8.
у = 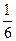 х3—
х3— 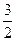 х2 + 8; у =
х2 + 8; у = 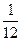 х3—
х3— 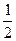 х2—3х + 10;
х2—3х + 10;
Вариант 9. Вариант 10.
у = 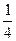 х3—
х3— 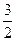 х2 + 2; у =
х2 + 2; у = 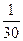 х3 +
х3 + 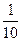 х2—
х2— 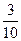 х + 2;
х + 2;
Вариант 11. Вариант 12.
у = 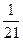 х3 +
х3 + 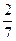 х2—3х +
х2—3х + 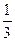 ; у =
; у = 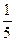 х3—
х3— 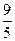 х2 + 3х + 3;
х2 + 3х + 3;
Вариант 13. Вариант 14.
у = 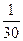 х3—
х3— 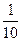 х2—
х2— 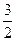 х + 1; у = -
х + 1; у = - 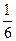 х3 +
х3 + 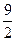 х + 2;
х + 2;
Вариант 15. Вариант 16.
у = 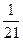 х3—
х3— 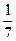 х2—
х2— 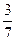 х —
х — 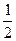 ; у = -
; у = - 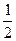 х3—6х — 1;
х3—6х — 1;
Вариант 17. Вариант 18.
у = - 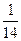 х3 +
х3 + 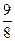 х2 + 3х — 6; у =
х2 + 3х — 6; у = 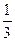 х3—
х3— 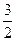 х2—4х;
х2—4х;
Вариант 19. Вариант 20.
у = 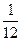 х3—
х3— 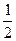 х2—3х; у =
х2—3х; у = 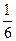 х3—
х3— 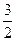 х2.
х2.
Интервалы монотонности и экстремумы функции одной переменной
Достаточное условие возрастания (убывания) функции на интервале 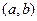 :
:
- если функция 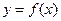 имеет производную на интервале
имеет производную на интервале 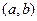 и во всех точках этого интервала выполняется
и во всех точках этого интервала выполняется
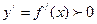
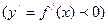 ,
,
то функция 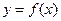 является монотонно возрастающей (убывающей) на этом интервале.
является монотонно возрастающей (убывающей) на этом интервале.

Рис.4.
Область решения неравенства 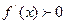 является областью монотонного возрастания функции
является областью монотонного возрастания функции 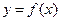 , а область решения неравенства
, а область решения неравенства 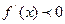 - областью монотонного убывания функции.
- областью монотонного убывания функции.
Точка х0 называется точкой максимума (max) функции 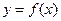 , если существует окрестность точки х0 такая, что для любого
, если существует окрестность точки х0 такая, что для любого 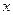
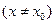 , принадлежащего этой окрестности, выполняется неравенство
, принадлежащего этой окрестности, выполняется неравенство 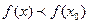 и точкой минимума (min), если
и точкой минимума (min), если 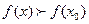 .
.
Значение функции в точке х0 называется соответственно максимум или минимум функции 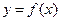 . Максимум и минимум имеют общее название "э кстремум " (рис.4).
. Максимум и минимум имеют общее название "э кстремум " (рис.4).
Необходимое условие экстремума можно сформулировать следующим образом:
- если функция 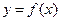 имеет экстремум в точке х0, то ее производная в этой точке
имеет экстремум в точке х0, то ее производная в этой точке 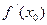 либо равна нулю, либо не существует.
либо равна нулю, либо не существует.
Пример: функция 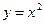 . Она имеет экстремум (минимум) в точке х0 =0. Производная этой функции
. Она имеет экстремум (минимум) в точке х0 =0. Производная этой функции 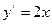 в точке х0 равна нулю.
в точке х0 равна нулю.
График функции 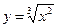 изображен на рис.5
изображен на рис.5
Из графика очевидно, что эта функция имеет экстремум (минимум) в точке х0 =0. Однако производная этой функции
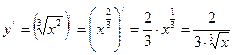
в точке х0 не существует, так как при х =0 знаменатель дроби обращается в ноль.
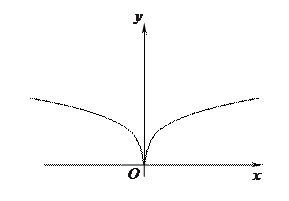
Рис.5. График функции 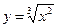
Необходимое условие экстремума не является достаточным, т.е. производная функции 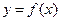 в точке х0 может быть равна нулю или не существовать, но между тем экстремума в этой точке нет. Так, например, производная функции
в точке х0 может быть равна нулю или не существовать, но между тем экстремума в этой точке нет. Так, например, производная функции 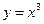
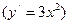 в точке х =0 равна нулю, но никакого экстремума в этой точке нет.
в точке х =0 равна нулю, но никакого экстремума в этой точке нет.
Первое достаточное условие экстремума.
Пусть х0 - критическая точка функции 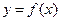 , и если при переходе через точку х0 слева направо
, и если при переходе через точку х0 слева направо 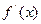 изменяет знак с "+" на "-", то в точке х0 - максимум, если с "-" на "+", то минимум. Если при переходе
изменяет знак с "+" на "-", то в точке х0 - максимум, если с "-" на "+", то минимум. Если при переходе 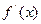 не изменяет знак, то экстремума в точке х0 нет.
не изменяет знак, то экстремума в точке х0 нет.
Второе достаточное условие экстремума, которое формулируется следующим образом.
Пусть в критической точке х0 производная функции 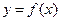 равна нулю, т.е.
равна нулю, т.е. 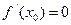 , и в этой точке существует вторая производная
, и в этой точке существует вторая производная 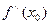 .
.
Тогда если
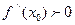 ,
,
то в точке х0 - минимум,
если 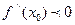 ,
,
то в точке х0 - максимум,
а если Ошибка! Ошибка связи.,
то экстремума в точке х0 нет.
Можно рекомендовать следующую схему исследования функции 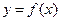 на экстремумы.
на экстремумы.
1. Найти выражение для 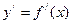 .
.
2. Найти критические точки функции, решив уравнение 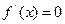 или определив значения хi, при которых
или определив значения хi, при которых 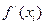 не существует, но существует исходная функция
не существует, но существует исходная функция 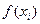 .
.
3. а) Исследовать изменение знака 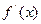 при переходе через каждую критическую точку хi и, использовав первое достаточное условие, определить, есть ли в этой точке экстремум и какой именно.
при переходе через каждую критическую точку хi и, использовав первое достаточное условие, определить, есть ли в этой точке экстремум и какой именно.
б) Если в критической точке 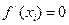 , то найти
, то найти 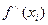 в этой точке и по ее знаку, использовав второе достаточное условие экстремума, определить наличие и характер экстремума.
в этой точке и по ее знаку, использовав второе достаточное условие экстремума, определить наличие и характер экстремума.
4. Найти значения экстремумов, подставив точки экстремумов хi в формулу 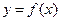 .
.
В ряде задач требуется найти наибольшее и наименьшее значения непрерывной функции 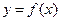 на некотором отрезке
на некотором отрезке 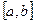 . По теореме Вейерштрасса эти значения достигаются
. По теореме Вейерштрасса эти значения достигаются
Рекомендуется следующая схема решения этой задачи.
1. Найти выражение для 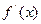 .
.
2. Найти критические точки функции 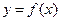 , принадлежащие отрезку
, принадлежащие отрезку 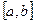 .
.
3. Найти значения функции 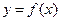 в критических точках.
в критических точках.
4. Найти значения функции на концах отрезка, т.е. 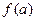 и
и 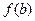 .
.
5. Выбрать из найденных значений по п.3, 4 наибольшее и наименьшее.
Выпуклость и вогнутость графика функции и точки перегиба
График функции 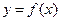 называется выпуклым (в некоторых книгах – выпуклым вверх) на интервале
называется выпуклым (в некоторых книгах – выпуклым вверх) на интервале 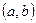 , если на этом интервале он лежит ниже любой своей касательной, и вогнутым (выпуклым вниз), если выше (рис.6).
, если на этом интервале он лежит ниже любой своей касательной, и вогнутым (выпуклым вниз), если выше (рис.6).
Точка, разделяющая интервал выпуклости и интервал вогнутости графика функции, называется точкой перегиба (графика) функции.
Можно доказать, что если 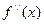 - вторая производная дважды дифференцируемой функции
- вторая производная дважды дифференцируемой функции 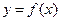 положительна на интервале
положительна на интервале 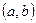 , то график вогнутый, а если
, то график вогнутый, а если 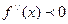 , то выпуклый на этом интервале. Это условие является достаточным условием выпуклости и вогнутости графика функции на рассматриваемом интервале.
, то выпуклый на этом интервале. Это условие является достаточным условием выпуклости и вогнутости графика функции на рассматриваемом интервале.
|
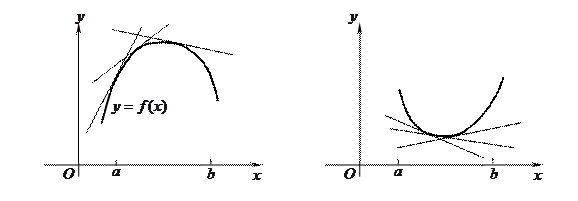
Рис.6. График функции 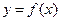
а – выпуклый (выпуклый вверх); б – вогнутый (выпуклый вниз)
Необходимое условие точки перегиба
Пусть х 0 - точка перегиба функции 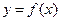 . В этой точке вторая производная
. В этой точке вторая производная 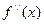 равна нулю или не существует.
равна нулю или не существует.
Точки, в которых выполняется необходимое условие точки перегиба, называются критическими точками второго рода функции 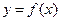 .
.
Достаточное условие точки перегиба формулируется следующим образом.
Пусть х 0 - критическая точка второго рода функции 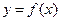 .Тогда если при переходе через эту точку
.Тогда если при переходе через эту точку 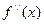 изменяет знак на противоположный, то х 0 - точка перегиба, а если не изменяет знак, то перегиба графика функции
изменяет знак на противоположный, то х 0 - точка перегиба, а если не изменяет знак, то перегиба графика функции 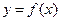 в точке х 0 нет.
в точке х 0 нет.
Изложим схему исследования функции 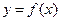 на выпуклость и точки перегиба графика.
на выпуклость и точки перегиба графика.
1. Найти выражение для 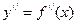 .
.
2. Найти критические точки второго рода функции, решив уравнение 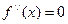 .
.
3. Решить два неравенства 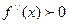 и
и 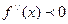 . При этом область решения неравенства
. При этом область решения неравенства 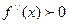 является областью вогнутости графика функции
является областью вогнутости графика функции 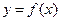 , а область решения неравенства
, а область решения неравенства 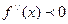 - областью выпуклости.
- областью выпуклости.
4. Определить, изменяет ли знак вторая производная функции при переходе через критические точки второго рода, и сделать вывод о наличии или отсутствии перегиба графика функции в этих точках. Найти значение функции в точке перегиба.
Исследование функции одной переменной и построение ее графика
При исследовании функции необходимо определить следующее.
1. Область определения функции.
2. Четность и периодичность.
3. Непрерывность, точки разрыва и их классификацию.
5. Интервалы монотонности и экстремумы.
6. Выпуклость и точки перегиба.
7. Некоторые дополнительные точки, уточняющие график (например, точки пересечения графика с осями координат и т.п.)
После этого выполнить построение графика.
5. Рекомендуемое содержание отчета (для студента).
1. Название лабораторной работы.
2. Цель и задачи исследований.
3. Электронно-вычислительные средства для расчетов.
4. Журнал (тетрадь) исследований (вычислений) с обработкой полученных данных в виде таблиц, графиков (по требованию).
5. Выводы.
6. Анализ и защита лабораторной работы производится индивидуально по результатам представленного отчета (перечень сделанного, представленные общие и индивидуальные задания, (формулы, основные свойства, график), ответы на рассмотренные в процессе выполнения контрольные вопросы.
Преподаватель оценивает знание каждого студента.
Литература
 2015-10-16
2015-10-16 1841
1841