Найти односторонние пределы

49.

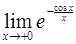
Ответ: 0

50.

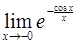
Ответ: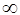

51.

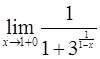
Ответ: 1

52.

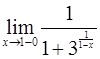
Ответ: 0

53.

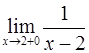
Ответ: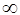

54.

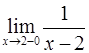
Ответ: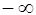

55.

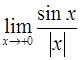
Ответ: 1

56.

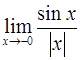
Ответ: -1

57.

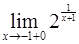
Ответ: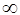

58.

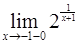
Ответ: 0

Исследовать функции на непрерывность

59. Найти точки разрыва функции

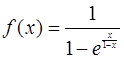
Решение:

Подозрительными на разрыв являются точки 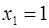и решение уравнения 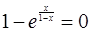, т.е.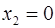

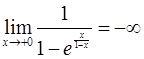
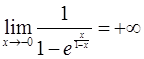
т.е. 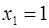– разрыв 2 рода;

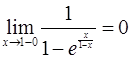
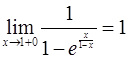
т.е. 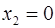– разрыв 1 рода.

60. Найти точки разрыва функции

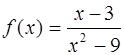
Ответ: 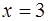– разрыв 1 рода;

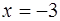– разрыв 2 рода.

61. Найти точки разрыва функции

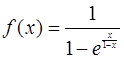
62. При каком значении 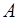будет непрерывной функция

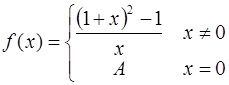
Решение:

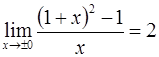Следует принять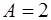

Элементы дифференциального исчисления

Контрольные вопросы к теме

1. Понятия приращения аргумента и приращения функции.

2. Производная функции, ее геометрический смысл.

3. Понятие дифференцируемости функции.

4. Дифференциал функции, его определение и геометрический смысл.

5. Понятие сложной и обратной функции.

6. Правила вычисления производных сложной и обратной функций.

7. Основные теоремы дифференцирования.

8. Раскрытие неопределенностей по правилам Лопиталя.

9. Производные высших порядков.