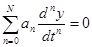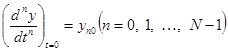Как известно, решение уравнения

, (5-3)

надо искать в виде

,

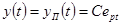где С, р — константы.

Подставляя это решение в (5-3) (дифференцируя п раз), после сокращения на общий множитель Се^pt получаем алгебраическое уравнение

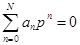, (5-4)

называемое характеристическим.

Так как (5-4) имеет ровно. N корней р ₁,..., р_N, каждый из которых дает решение (5-3), то учитывая, что сумма решений также является решением,

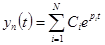. (5-5)

В общем случае корни р_i, являются комплексными. Поскольку характеристическое уравнение имеет действительные коэффициенты, то корни являются комплексно-сопряженными: 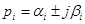.Каждая пара корней дает в выражении (5-5) составляющую, равную

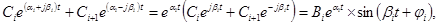
где В_i, φ_i, определяются через С_i и С_{i+ 1}

При α_i <0 эта составляющая будет затухать во времени (рис. 5-2,а), при a_i >0 — нарастать (б), а при a_i =0 получим незатухающие колебания (в) или постоянную составляющую (если β_i =0). Таким образом, исследуемый процесс состоит из суммы апериодических или колебательных составляющих. Понятно, если каждая составляющая будет затухать (все a_i <0), то и переходная составляющая затухнет со временем. Однако, если хотя бы один корень имеет положительную действительную

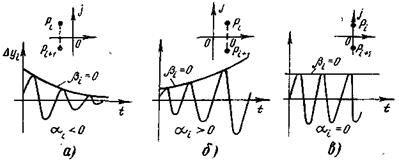
Рис. 5-2. Связь устойчивости с корнями характеристического уравнения системы

часть, но переходная составляющая будет нарастать во времени, что соответствует неустойчивой системе. При a_i =0 система находится на границе устойчивости.

Если характеристическое уравнение (5-4) имеет порядок 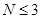, то корни можно найти аналитически, однако для 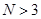нахождение корней затруднительно. Нас выручает тот факт, что для исследования устойчивости надо знать не сами корни, а лишь знаки действительных частей и даже менее того — все ли корни лежат слева от мнимой оси или есть хотя бы один справа. Правила, позволяющие ответить на этот вопрос, не находя самих корней, называются критериями устойчивости. Последние могут быть алгебраическими (суждение об устойчивости выносится по рассмотрению характеристического уравнения) и частотными (об устойчивости судят по частотным характеристикам системы). Прежде чем рассмотреть критерии устойчивости, обратим внимание на вид характеристического уравнения (5-4): правая часть его совпадает со знаменателем передаточной функции исследуемой системы. Как было указано в гл. 4, в результате структурных преобразований линейную систему можно привести к типовому виду (см. рис. 4-16). Замечаем, что передаточная функция разомкнутой системы (разрыв обратной связи) равна

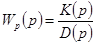, (5-6)

а для замкнутой —,

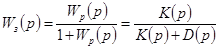
Поэтому характеристическое уравнение имеет вид:

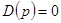(5-7)

— для разомкнутой системы,

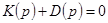(5-8)

для замкнутой системы.