Пусть функции U(x) и V(x) имеют непрерывные производные на [a;b], тогда справедлива формула
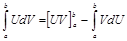 . (3)
. (3)
Пример 2. Вычислить: 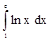 .
.
Решение: пусть 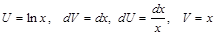 , т. к. функции
, т. к. функции 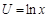 и
и 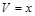 непрерывны на
непрерывны на 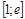 вместе со своими производными, то согласно формуле (I) находим
вместе со своими производными, то согласно формуле (I) находим
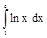
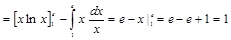 .
.
Пусть функции U(x) и V(x) имеют непрерывные производные на [a;b], тогда справедлива формула
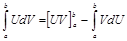 . (3)
. (3)
Пример 2. Вычислить: 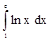 .
.
Решение: пусть 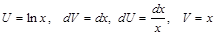 , т. к. функции
, т. к. функции 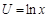 и
и 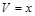 непрерывны на
непрерывны на 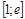 вместе со своими производными, то согласно формуле (I) находим
вместе со своими производными, то согласно формуле (I) находим
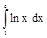
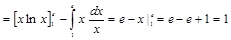 .
.
|
|
