Рассмотрим плоскую материальную фигуру, ограниченную прямыми х=а, x=b (a<b) и кривыми y= 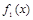 ,
, 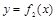 , где функции
, где функции 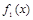 и
и 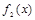 непрерывны на
непрерывны на 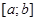 и
и 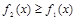 :
:
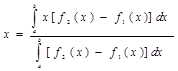 ,
, 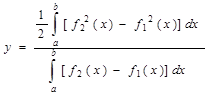 , где
, где 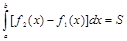 (площадь фигуры).
(площадь фигуры).
Если фигура ограничена осью ОХ, прямыми х=а, х=b и кривой y= f (x), где f (x) – неотрицательная непрерывная на отрезках [a; b]  функция, то полученные формулы будут проще:
функция, то полученные формулы будут проще:
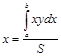 ;
; 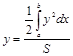 .
.
Если фигура располагается симметрично относительно некоторой прямой, то центр тяжести ее лежит на этой прямой.
Пример 15. Найти координаты центра тяжести фигуры, ограниченной кривой 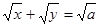 и осями координат.
и осями координат.
Т.к. данная фигура симметрична относительно биссектрисы I координатам угла, то ее центр тяжести лежит на этой прямой у=х, и следовательно, 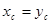 ;
;
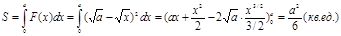
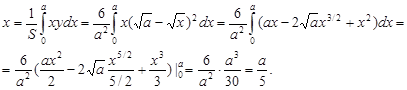
Ответ: 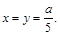
 2015-10-13
2015-10-13 684
684








