План:
1. Представление информации в многомерном пространстве.
2. Ранговые методы. Ранговая корреляция. Таблица сопряженности.
3. Дисперсионный анализ влияния качественных факторов.
4. Факторный анализ. Метод главных факторов.
5. Многомерное шкалирование. Классическая модель многомерного шкалирования.
6. Неметрические методы МНШ.
7. Кластерный анализ.
1. Представление информации в многомерном пространстве.
Методы многомерного статистического анализа (МСА) основываются на геометрическом представлении информации. Исследуемые объекты рассматриваются в теоретическом пространстве размерностью, соответствующей числу признаков (элементарных или латентных), которыми они характеризуются. Можно предложить частные случаи признакового пространства: с нулевой размерностью – объекты не имеют характеристик; с единичной размерностью (одинарное признаковое пространство) – объекты отражаются значениями одного какого-либо признака; многомерное пространство – объекты отражаются двумя и более признаками (m– мерное признаковое пространство).
Рассмотрим простой пример, когда пять домохозяйств последовательно характеризуются значениями одного, двух, трех признаков.
1. Одномерное признаковое пространство.
Таблица 4.1.1
| Домохозяйство | Средний уровень потребления мяса в месяц на одного человека, кг. (х) |
Его можно представить в виде одной градуированной шкалы:
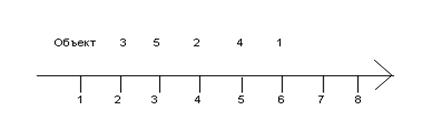
Рис.4.1.1
2.Двумерное признаковое пространство.
Таблица 4.1.2
| Домохозяйство | Средний уровень потребления мяса в месяц на одного человека, кг. (х) | Средний уровень потребления молока на одного человека, л (х2) |
Наблюдаемые объекты геометрически представляются на плоскости в двумерной (декартовой) системе координат.
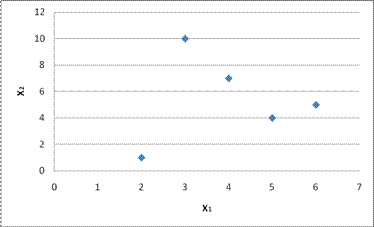
Рис.4.1.2
3.Трехмерное признаковое пространство.
Таблица 4.1.3
| Домохозяйство | Средний уровень потребления мяса в месяц на одного человека, кг. (х) | Средний уровень потребления молока на одного человека, л (х2) | Среднее потребление сахара и кондитерских изделий на одного человека, кг. (х3) |
| 1,2 | |||
| 1,9 | |||
| 3,5 | |||
| 2,7 | |||
| 2,8 |
Наблюдаемые объекты представляются в трехмерной системе координат.
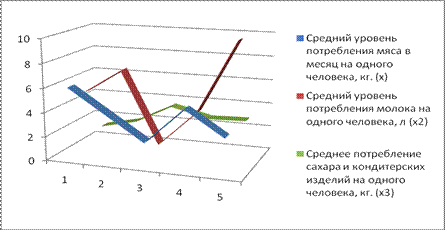
Рис. 4.1.3
Характеристика и пространственное представление наблюдаемых объектов: предприятий, территорий, групп населения и т.д. по значениям признаков – это наиболее распространенная и привычная форма организации статистических данных. Однако в многомерной статистике возможны и достаточно часто встречаются случаи с другой организацией данных, когда оцениваемые признаки сами выступают в качестве наблюдаемых объектов и помещаются в теоретическое пространство предприятий, территориальных единиц и т.д.
Изменим в предыдущем примере исходное условие: пусть требуется характеристика признаков по домохозяйствам. Для наглядности отберем два первых домохозяйства и покажем возможность размещения их на координатной плоскости признаковых значений:
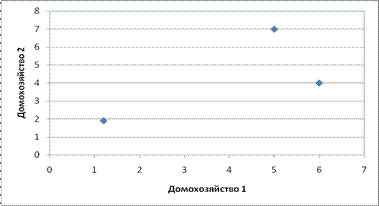
Рис. 4.1.4
Размерность пространства описывается при помощи сокращения слова dimension – размерность, как dim U, то есть размерность пространства U. Частными случаями многомерного пространства являются 0-мерное пространство – пространство, не содержащее признаков, или объектов, dim U0 – 0, и одномерное пространство dim U1 – 1. В общем случае dim U – р.
В многомерном пространстве признаки или объекты, имеют определенные количественные характеристики. Все принимаемые значения признаков (объектов) представляют собой множества вещественных чисел, и при этом множество обозначают символом Rp, где р по-прежнему указывает размерность пространства.
В аналитической работе при обращении к многомерному пространству признаков (объектов) принимаются во внимание следующие особенности.
· В р-мерном пространстве сохраняют свою силу положения евклидовой геометрии. Например, в прямоугольной системе координат углы между всеми парами осей составляют 900, параллельные прямые, плоскости и гиперплоскости не пересекаются, если квадрат расстояния между двумя точками в двумерном пространстве определяется по известной формуле Пифагора: с2 = 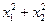
 , то в многомерном пространстве – аналогичным образом с2 =
, то в многомерном пространстве – аналогичным образом с2 = 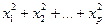 .
.
· Пространство, размерность которого превышает три, уже не может быть представлено визуально, и все задачи в этом случае решаются при помощи абстрактной логики и алгебраических методов.
· В многомерном анализе, как правило, используется большое число признаков, разнородных по своей природе. В связи с этим на первом этапе исследований обычно возникает проблема приведения всех анализируемых признаков к одному основанию – сопоставимому виду. Подобные проблемы решают нормированием данных, что геометрически означает изменение масштаба и другие преобразования координатной системы.
· При работе с р-мерными данными совместно используются математические, абстрактные методы и методы экономико-статистического анализа, ориентированные на конкретные сферы приложения. Следует обращать внимание на непротиворечивость результатов, полученных различными методами. Возникающие противоречия указывают на нарушения логики решения экономической задачи и становятся зачастую источником ошибочных выводов.
2. Ранговые методы. Ранговая корреляция. Таблица сопряженности.
При изучении неколичественных признаков или количественных признаков с непрерывными и неизвестными законами распределения классический подход корреляционного анализа оказывается неэффективным, и в этих случаях применяют методы непараметрической статистики и, в частности, метод ранговой корреляции.
Ранговая корреляция предназначена для изучения статистической связи между различными упорядочиваниями (ранжированиями) объектов по степени проявления в нем того или иного свойства.
Пусть Х(j) = (x1(j), x2(j), …xn(j)) некоторая ранжировка из n объектов по j – тому свойству. Компонента xi(j), i=1,…,n этой ранжировки определяет порядковое место (ранг) которое присвоено i–му объекту в общем ряду n анализируемых объектов, упорядоченных по убыванию j –го свойства. Другая ранжировка Х(k) = (x1(k), x2(k), …xn(k)) может интерпретироваться либо как упорядочивание объектов по другому k-му свойству, либо как ранжировка по этому же свойству, но полученная другим экспертом.
Ранговый коэффициент корреляции Спирмена измеряет степень согласованности двух различных ранжировок Х(j) и Х(k) одного и того же множества из n объектов и рассчитывается по формуле:
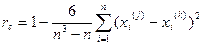 (4.2.1)
(4.2.1)
Причем, -1£ rc £1. -1 означает, что ранжировки противоположны, 1 – что они совпадают. Если rc=0, связь отсутствует.
Связанные ранги возникают в случае дележки мест в ранжировке. Объектам, которые делят места, приписывается ранг, равный среднему арифметическому соответствующих мест. Например, если обекты делят места с 3 по 5, то ранг равен среднеарифметическому этих мест – 4 ((3+4+5)/3) и объектам, находящимся на 3-5 местах приписывается ранг 4.
Для связанных рангов формула коэффициента корреляции Спирмена усложняется:
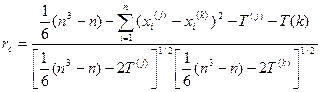 , (4.2.2)
, (4.2.2)
где Т( l )= 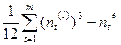 , здесь m – число групп, для которых имеются связанные ранги, nt – число рангов, входящих в t – ю группу.
, здесь m – число групп, для которых имеются связанные ранги, nt – число рангов, входящих в t – ю группу.
Проверка гипотезы Н0: rc=0. если n>10, то статистика 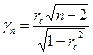 распределена по закону Стьюдента с (n-2) степенями свободы.
распределена по закону Стьюдента с (n-2) степенями свободы.
При 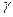 n>t
n>t 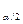
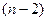 гипотеза Н0 отклоняется, иначе – не отклоняется. Если n£10, то рассчитывают rcmax=
гипотеза Н0 отклоняется, иначе – не отклоняется. Если n£10, то рассчитывают rcmax= 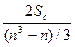 , где S извлекается из таблицы для уровня значимости
, где S извлекается из таблицы для уровня значимости 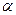 /
/ 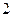 и если |rc|> rcmax, то Н0 отвергается.
и если |rc|> rcmax, то Н0 отвергается.
Ранговый коэффициент корреляции Кендала.
Расчетная формула имеет вид:
rk = 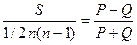 , S=P-Q (4.2.3)
, S=P-Q (4.2.3)
Ранжируем все элементы по признаку х(1), по ряду другого признака х(2), подсчитываем для каждого ранга число последующих рангов, превышающих данный (их сумму обозначим Р) и число последующих рангов ниже данного (их сумму обозначим через Q). Значения коэффициента -1£ rk £1.
На практике при n³10, rc 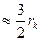 . Для связанных рангов формула коэффициента корреляции Кендала имеет вид
. Для связанных рангов формула коэффициента корреляции Кендала имеет вид
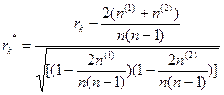 ,
, 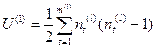 , l =1,2 (4.2.4)
, l =1,2 (4.2.4)
Коэффициент конкордации (согласованности) Кендала.
Измеряет степень тесноты статистической связи между различными ранжировками:
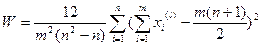 (4.2.5)
(4.2.5)
Причем 0<W<1, если W=1 – ранжировки совпадают, W=0 связь между ранжировками отсутствует.
Для связанных рангов
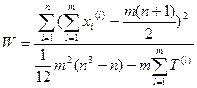 (4.2.6)
(4.2.6)
Проверка гипотезы Н0:W =0 при n>7 рассчитывают статистику 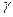 n=m(n-1)W и при
n=m(n-1)W и при 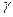 n>
n> 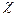
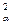 (n-1) гипотеза отклоняется, иначе не отклоняется.
(n-1) гипотеза отклоняется, иначе не отклоняется.
Корреляция категоризованных переменных
Признак называется категоризованным, если его возможные «значения» описываются конечным числом состояний (категорий, градаций). В этом случае для двух категоризованных признаков исходные данные представляются в виде таблиц сопряженности.
Таблица 4.2.1
| Градации признака х (1) | Градации признака х(2) | ni | |||||
| …. | j | … | m2 | ||||
| n11 | n12 | …. | n1j | …. | n1m2 | n1. | |
| n21 | n22 | …. | n2j | …. | n2m2 | n2. | |
| … | …. | …. | …. | …. | …. | ||
| i | ni1 | ni2 | …. | nij | …. | nim2 | ni |
| … | …. | …. | |||||
| m1 | nm11 | nm12 | …. | nn1j | …. | nm1m2 | nm1. |
| n.j | n.1 | n.2 | …. | n.j | …. | n.m2 | n. |
В таблице nij – число объектов (из общего числа n обследованных), у которых «значение» признака х(1) на i-м уровне градации, а «значение»0 признака х(2) на j-м уровне. Также ni. = ∑ nij – число объектов, значение признака х(1) у которых на i-й градации (i=1,2,…,m1); n.j=∑ nij - число объектов, значение признака х(2) у которых на j-й градации (j=1,2,…,m2).
Одним из основных измерителей степени тесноты статистической связи между категоризованными переменными может служить коэффициент взаимной сопряженности А.Чупрова.
Коэффициент взаимной сопряженности А.А.Чупрова применяется для измерения тесноты связи качественных признаков и рассчитывается по формуле
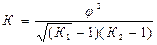 , (4.2.7)
, (4.2.7)
где К1 – обозначает число возможных значений первой статистической величины (число групп),
К2 – число возможных значений второй статистической величины,
φ 2 – показатель взаимной сопряженности, который определяется как сумма отношений квадратов частот каждой клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы единицу, получим величину φ 2 .
Рассмотрим пример расчета коэффициента взаимной сопряженности и составления таблиц сопряженности.
Условие задачи: по крестьянскому хозяйству имеются данные о внесении удобрения в почву и урожайности по 60 участкам:
Таблица 4.2.2
| Степень удобрения почвы | Урожайность | ||
| Низкая | Высокая | Итого | |
| Низкая | |||
| Высокая | |||
| Итого |
Вычислительная работа φ 2 производится по следующей схеме (см. табл. ниже):
Таблица 4.2.3
| Степень удобрения почвы | Урожайность | ||
| Низкая | Низкая | Итого | |
| Низкая | (256) 11,64 | (100) 2,63 | 14,27 0,548 |
| Высокая | (36) 1,63 | (784) 20,63 | 22,76 0,669 |
| Итого | 1,1273 |
Сначала, в верхней части каждой клетки этой схемы записывают частоты таблицы распределения данной задачи. Под ними (в скобках) записываются квадраты этих частот. Затем производят деление каждого квадрата на итог частот соответствующего столбца (256:22). Полученные результаты записывают в нижней части соответствующих клеток.
После этого числа, записанные внизу каждой клетки, суммируются для каждой строки, суммы записываются в нижней части клеток итогового столбца (11,64+2,63=14,27). Наконец, эти суммы 14,27; 22,76 делятся на соответствующие итоги строк 26,34 и полученные частные 0,548 и 0,669 записываются в последнем столбце таблицы. Сумма этих чисел 1,217, без единицы, представляет собой φ 2. таким образом,
φ 2 =1,217-1=0,217.
Теперь вычислим коэффициент взаимной сопряженности А.А.Чупрова по формуле
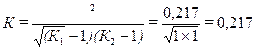 .
.
К1 и К2 равны 2, так как таблица двухклеточная.
3. Дисперсионный анализ влияния качественных факторов.
Статистический метод, предназначенный для выявления влияния нескольких одновременно действующих факторов на исследуемый показатель (наблюдаемую величину).
Сам термин был введен в статистическую практику английским аналитиком Р.Фишером (1925г.) и изначально широко использовался при проведении сельскохозяйственных экспериментов.
Дисперсионный анализ позволяет при сравнительно малом числе измерений независимо оценить влияние каждого из факторов на измеряемый количественный показатель. Сами факторы могут быть и качественными и количественными. Применение дисперсионного анализа при пассивных наблюдениях, например, в экономике, подразумевает надлежащий отбор групп данных из более богатой совокупности данных.
В основе данного анализа лежит следующая вероятностная модель:
Yj=xijq1 +…+xmjqn+ej, j=1,…,n, (4.3.1)
Где qa - неизвестный параметр, отражающий влияние переменной хa на измеряемую величину у, индекс j помечает номер измерения. Ошибки ej предполагаются случайными величинами с нулевыми средними, постоянной дисперсией 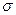 2 и независимыми в совокупности, распределенными по нормальному закону.
2 и независимыми в совокупности, распределенными по нормальному закону.
В дисперсионном анализе переменные хa принимают целочисленные значения, обычно это 0 и 1. При непрерывном изменении этих факторов, приведенная выше модель относиться к регрессионному анализу. Если в нее входят факторы обоих видов, то говорят о ковариационном анализе. Очевидно, что все три случая поглощаются регрессионным анализом.
Иногда параметры модели qa являются случайными факторами. Термин «смешанная модель» применяют, когда в нее входят случайные и постоянные параметры qa.
Различают однофакторный и многофакторный дисперсионный анализ.
Однофакторный анализ.
Несмотря на свою простоту он иллюстрирует основные идеи дисперсионного анализа. Модель однофакторного дисперсионного анализа выглядит следующим образом
Yij = mi +eij, i=1,..,m; j=1,…,ni, (4.3.2)
где mi = xijqi; xij= 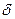 ij; eij удовлетворяет тем же требованиям, что и ei.
ij; eij удовлетворяет тем же требованиям, что и ei.
Одной из наиболее популярных нулевых гипотез Н, проверяемых в рамках дисперсионного анализа является гипотеза о равенстве всех mi. Параметр mi может быть, например, производительностью i-го предприятия, урожайностью i-ой сельскохозяйственной культуры и т.д.
Модель однофакторного дисперсионного анализа может быть проанализирована в рамках регрессионного анализа через оценивание параметров qi..
Основная идея проверки гипотезы Н заключается в следующем: строятся две независимые оценки дисперсии случайной величины e, одна из которых предполагает выполнение гипотезы Н, а другая – нет. Затем составляется их отношение, которое должно иметь центральное F-распределение при выполнении Н и нецентральное F-распределение с параметром нецентральности, определяемым разбросом (дисперсией) параметров bi.
Независимые оценки дисперсии случайной величины e можно записать в виде следующих формул:
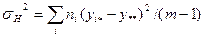 (4.3.3)
(4.3.3)
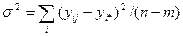 , (4.3.4)
, (4.3.4)
Где 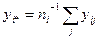 ;
; 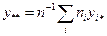 ;
; 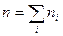 , т.е. отклонение
, т.е. отклонение
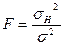 (4.3.5)
(4.3.5)
Имеет F- распределение с m-1 и n-m степенями свободы. Параметр нецентральности равен:
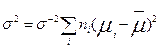 , (4.3.6)
, (4.3.6)
где 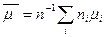 .
.
По F- критерию гипотеза Н отвергается с уровнем значимости a, если F>Fa,m-1,n-1. Параметр s2 определяет мощность F-критерия.
Во многих исследованиях по дисперсионному анализу модель однофакторного анализа записывается следующим образом:
yij=m+ai+eij; 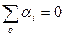 (4.3.7)
(4.3.7)
Тогда гипотеза Н предполагает, что все ai равны. Модель в таком виде более удобна при рассмотрении задач многофакторного дисперсионного анализа.
Предположим, что анализируя производительность i-го предприятия нужно оценить эффект использования j-ой технологии. Тогда, по аналогии с приведенной выше моделью, целесообразно рассматривать следующую модель:
yijk=m+ai+bi+(ab)ij+eijk, 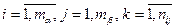 . (4.3.8)
. (4.3.8)
Константа (ab)ij называется парным взаимодействием факторов ai и bj.
В рамках данной модели можно сформулировать довольно много гипотез, достойных экспериментальной проверки. Наиболее популярны следующие:
НА: ai=0, 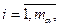 (4.3.9)
(4.3.9)
НВ: bi=0, 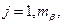 (4.3.10)
(4.3.10)
НАВ: (ab)ij=0, 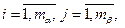 (4.3.11)
(4.3.11)
Например, гипотеза НАВ может трактоваться как гипотеза о несущественности того, на каком предприятии какие технологии используются для производства.
Идея проверки гипотезы так же, как и в однофакторном анализе, состоит в построении независимых оценок для дисперсии случайной величины e. Причем, оценки конструируются в предположении справедливости или гипотезы НA или НВ, или НАВ, или НА и НВ вместе и т.д.
Можно построить модели и для большего числа факторов. Следует лишь иметь в виду, что при нескольких факторах можно (но необязательно) ввести тройные, четвертные и т.д. взаимодействия. Обычно независимо от количества анализируемых факторов ограничиваются лишь парными взаимодействиями.
В отличие от однофакторного случая при многофакторном дисперсионном анализе не любое распределение наблюдений nij по ячейкам (i,j,…) позволяет конструировать независимые оценки для s2  при различных гипотезах. Задача разумного выбора Нij составляет один из важнейших разделов математической теории планирования эксперимента.
при различных гипотезах. Задача разумного выбора Нij составляет один из важнейших разделов математической теории планирования эксперимента.
Особый практический интерес эта задача представляет при значительном количестве факторов. Предположим, что в каждой из ячеек i,j,… проводятся n0 наблюдений. легко убедиться в необходимости n0, ms, mb …наблюдений для реализации всего эксперимента. Использование специальных планов позволяет резко сократить количество необходимых наблюдений.
4. Факторный анализ
Факторный анализ – это один из разделов многомерного статистического анализа. Он содержит и разрабатывает вычислительные методы, которые на основе обработки больших массивов информации позволяют выявить скрытые обобщенные факторы, которые в достаточной степени объясняют поведение исследуемого показателя (показателей).
Следовательно, отличительной особенностью факторного анализа является то, что он не основывается на априорно заданном перечне показателей, характеризующих исследуемый объект, а позволяет обнаружить существенные факторы, которые первоначально «не видны» не очевидны, не наблюдаемы. Например, на размер прибыли оказывают непосредственное влияние денежная выручка и себестоимость. Но в процессе исследования может оказаться, что существенными, но опосредованными (скрытыми) факторами, влияющими на размер прибыли являются методика планирования и система организации производства.
Выявленные скрытые факторы позволяют записать уравнение регрессии с относительно небольшим количеством коэффициентов.
Большое значение этих факторов позволяет использовать их как управляемые. Ни число этих факторов, ни вид их преобразования в наблюдаемые переменные не известны и должны определяться в результате проведения факторного анализа только из наблюдаемых факторов.
К основным задачам, связанным с построением модели факторного анализа относятся задачи существования и идентификации (единственности) модели, статистического оценивания неизвестных параметров и их алгоритмического определения, а также статистической проверки гипотез об адекватности модели наблюдаемым данным, о значениях структурных параметров и т.п.
Факторный анализ является более общим методом преобразования исходных переменных по сравнению с компонентным анализом. Модель факторного анализа имеет вид:
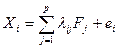 , (4.4.1)
, (4.4.1)
где lij – постоянные величины, называемые факторными нагрузками,
Fj – общие факторы, используемые для представления всех р исходных переменных,
еi – специфические факторы, уникальные для каждой переменной, р £ т.
Задачами факторного анализа являются: определение числа общих факторов, определение оценок l, определение общих и специфических факторов. Для получения оценок общностей и факторных нагрузок используется эмпирический итеративный алгоритм, сходящийся к истинным оценкам параметров, суть которого сводится к следующему:
1. Первоначальные оценки факторных нагрузок определяются с помощью метода главных факторов. На основании корреляционной матрицы R формально определяются оценки главных компонент:
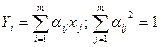 , i=1,…,т. (4.4.2)
, i=1,…,т. (4.4.2)
2. Оценками факторных нагрузок служат величины
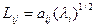 , i=1,…,т; j=1,…,p, (4.4.3)
, i=1,…,т; j=1,…,p, (4.4.3)
где aij – оценки aij; Lij – оценки l ij.
4. Оценки общностей получаются как
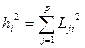 . (4.4.4)
. (4.4.4)
5. На следующей итерации модифицируется матрица R – вместо элементов главной диагонали подставляются оценки общностей, полученные на предыдущей итерации; на основании модифицированной матрицы R c помощью вычислительной схемы компонентного анализа повторяется расчет главных компонент (которые не являются таковыми с точки зрения компонентного анализа), ищутся оценки главных факторов, факторных нагрузок, общностей, специфичностей. Факторный анализ можно считать законченным, когда на двух соседних итерациях оценки общностей меняются слабо.
Преобразования матрицы R могут нарушать положительную определенность матрицы R и как следствие некоторые собственные значения R могут быть отрицательными. Для лучшей интерпретации полученных общих факторов к ним применяется процедура варимаксного вращения.
Если факторный анализ ведется в терминах главных компонент, то значения факторов могут быть вычислены непосредственно. Главные компоненты (без вращения) могут быть представлены в виде:
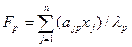 , р=1,…,т, (4.4.5)
, р=1,…,т, (4.4.5)
где ajp – коэффициенты при общих факторах,
lр- собственные значения,
хj – исходные данные (вектор-столбцы),
Fp – главные компоненты.
В случае вращения главных компонент соотношения, связывающие исходные переменные и значения факторов, несколько усложняются. Ниже в матричном виде приведено соотношение, оптимальное по скорости вычисления, а также не зависимое от метода вращения факторов:
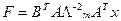 ,
,
где ВТ – повернутая матрица А, А – матрица коэффициентов при общих факторах; L т – диагональная матрица т собственных членов; x – матрица исходных данных; F – матрица т повернутых факторов.
При определении числа общих факторов руководствуются следующими критериями: число существенных факторов можно оценить из содержательных соображений, в качестве р берется число собственных значений, больших либо равных единице (по умолчанию), выбирается число факторов, объясняющих определенную часть общей дисперсии или суммарной мощности.
Известны линейные и нелинейные модели факторного анализа. Однако задачи идентификации таких моделей теоретически не решены и не известны свойства получаемых оценок. Факторный анализ при конкретной реализации связан со значительными затратами времени компьютера из-за громоздкости вычислительных процедур, сложности итерационных процессов и, как правило, больших размеров матрицы исходных данных.
На практике факторный анализ обычно используется, во-первых, как метод свертки информации с целью понижения размерности пространства наблюдаемых переменных, во-вторых, как метод выделения источников вариации матрицы наблюдений, исключающий вариацию ошибок, и, наконец, как метод классификаций многомерных наблюдений.
Факторный анализ находит широкое применение в экономических исследованиях, таких как анализ систем экономических показателей, построение обобщающих показателей экономического и социально-экономического развития фирм, регионов, стран, классификация экономических объектов, анализ спроса и предложения и др.
5. Многомерное шкалирование. Классическая модель многомерного шкалирования.
Многомерное шкалирование – это совокупность математических методов, позволяющих по заданной информации о мерах различия (близости) между объектами рассматриваемой совокупности приписывать каждому из этих объектов вектор характеризующих его количественных показателей. При этом размерность искомого координатного пространства задается заранее, а «погружение» в него анализируемых объектов производится таким образом, чтобы структура взаимных различий (близостей) между ними, измеренных с помощью приписываемых им вспомогательных координат, в среднем ……….. отличалась бы от заданной в смысле того или иного функционала качества.
Процедуры многомерного шкалирования применяются, когда данные заданы в виде матрицы попарных расстояний между объектами или их порядковых отношений. В первом случае используются методы так называемого метрического шкалирования, а во втором – неметрического шкалирования.
Задача многомерного шкалирования относится к ситуации, когда исследуемая совокупность элементов задана с помощью матрицы попарных расстояний и заключается в приписывании каждому из элементов заданного числа (р) координат таким образом, чтобы структура попарных взаимных расстояний между элементами, измеренных с помощью этих вспомогательных координат, в среднем незначительно отличались бы от заданной.
Основные типы задач, решаемые МНШ:
- поиск и интерпретация латентных переменных, объясняющих заданную структуру попарных расстояний. Этот тип задач предусматривает не только построение вспомогательных шкал (координатных осей), в системе которых затем рассматриваются анализируемые объекты, но и содержательную интерпретацию этих шкал:
- верификация геометрической конфигурации системы анализируемых объектов в координатном пространстве латентных переменных;
- сжатие исходного массива данных с минимальными потерями в их информативности.
МНШ можно рассматривать как альтернативу факторному анализу. Как известно целью факторного анализа является поиск и интерпретация латентных переменных, дающих возможность объяснить сходства между объектами в исходном пространстве признака. В факторном анализе сходства (различия) между объектами выражаются с помощью матрицы коэффициентов корреляций.
В методе МНШ наряду с корреляционными матрицами в качестве исходных данных используется произвольный тип матрицы сходства объектов.
На входе алгоритма МНШ – матрица, элементы которой содержат сведения о попарном сходстве (различии) анализируемых объектов. На выходе алгоритма получаются числовые значения координат которые приписываются каждому объекту в некоторой новой системе координат (во вспомогательных шкалах, связанных с латентными переменными), причем размерность нового пространства признаков меньше размерности исходного.
Основной тип данных в многомерном шкалировании – меры близости между двумя объектами, измеряющие насколько эти объекты похожи. Наиболее часто используются коэффициенты корреляции и совместные вероятности.
Обозначим меру близости двух объектов i и j как dij. Если самые большие значения dij соответсвуют парам наиболее похожих объектов то dij - мера сходства, если же – парам ниаменее похожих объектов – то dij - мера различия.
Необходимо, чтобы исходные данные представляли матрицу расстояний между объектами 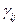 ,то есть, выполнен набор аксиом расстояний:
,то есть, выполнен набор аксиом расстояний:
1. 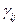 ≥ 0,
≥ 0, 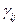 = 0, i,j= 1,2,….n;
= 0, i,j= 1,2,….n;
2. 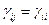 , i,j= 1,2,….n;
, i,j= 1,2,….n;
3. 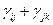 ≥
≥ 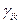 , i,j, k= 1,2,….n.
, i,j, k= 1,2,….n.
Как правило, матрицы строятся на основе опроса экспертов с использованием шкал сравнения или в категоризованной форме. В этом случае условие 1 выполняется, а свойства 2 и 3 оказываются нарушенными. Для выполнения свойства 2 полагают, что
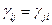 = ½(
= ½(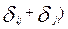 (4.5.1)
(4.5.1)
Если для 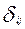 выполнены все свойства, кроме 3, то можно определить величину D =
выполнены все свойства, кроме 3, то можно определить величину D = 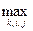 (
(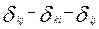 )
)
и затем 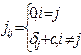 (4.5.2)
(4.5.2)
Если каждый из объектов задан набором числовых характеристик vi1,……,viq и они одинаково важны для формирования различий объектов, то расстояние может быть определено как
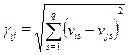 , i,j = 1,2,……., n (4.5.3)
, i,j = 1,2,……., n (4.5.3)
Пусть исходная информация об объектах задана в форме матрицы попарных сравнений 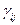
Если заданы коэффициенты корреляции, то можно положить 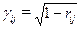 , i,j = 1,2,….n
, i,j = 1,2,….n
В классической модели МНШ, предложенной У.Торгерсоном, предполагается, что по этой матрице можно построить точки 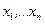 в пространстве некоторого небольшого числа измерений р, причем так, чтобы каждый элемент матрицы
в пространстве некоторого небольшого числа измерений р, причем так, чтобы каждый элемент матрицы 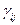 представлял собой евклидово расстояние
представлял собой евклидово расстояние
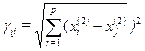 (4.5.4)
(4.5.4)
между объектом i и объектом j, то есть в матричном виде:
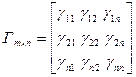 (4.5.5)
(4.5.5)
Неизвестны координаты объектов:
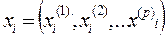 , i=1,…,n (4.5.6)
, i=1,…,n (4.5.6)
Требуется на основании известных расстояний вида (4.5.5) восстановить неизвестную размерность р пространства признаков и приписать каждому объекту координаты (4.5.6) так, чтобы вычисленные евклидовы расстояния совпали с заданными (4.5.5).
Таким образом, цель МНШ состоит в том, чтобы преобразовать информацию о конфигурации исходных многомерных данных, заданную матрицей расстояний в геометрическую конфигурацию точек в многомерном пространстве.
Модель предполагает, кроме того, что 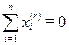 , r=1,…, р
, r=1,…, р
Введем матрицу центрированных значений координат объектов:
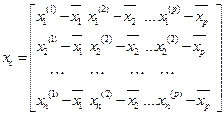
И матрицу такую, что
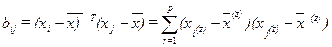 (4.5.6)
(4.5.6)
Элементы матрицы В и Г связаны соотношением:
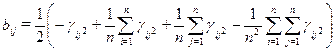 (4.5.7)
(4.5.7)
Выражение (4.5.6) представляет собой теорему У.Торгерсона.
Матрица В обладает следующими свойствами:
- неотрицательно определена;
- ранг матрицы равен размерности р искомого пространства;
- ненулевые собственные числа матрицы, упорядоченные по убыванию, совпадают с собственными числами матрицы 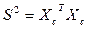
- обозначим 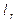 , r = 1,…, р собственный вектор, соответствующий собственному значению
, r = 1,…, р собственный вектор, соответствующий собственному значению 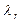 матрицы
матрицы 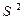 . Тогда вектор
. Тогда вектор 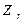 значений r-й главной компоненты вектора Х будет определяться по правилу
значений r-й главной компоненты вектора Х будет определяться по правилу 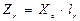 . Причем, если
. Причем, если 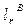 - собственный вектор матрицы В, соответствующий тому же собственному числу
- собственный вектор матрицы В, соответствующий тому же собственному числу 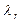 , то
, то
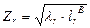 , r = 1,…,р (4.5.8)
, r = 1,…,р (4.5.8)
Таким образом из свойства матрицы В следует, что находя собственные числа и собственные векторы этой матрицы, получим координатное пространство (r) анализируемых объектов в пространстве главных компонент искомого многомерного признака Х, что и является решением задачи МНШ. Из свойств матрицы В также следует, что ее элементы могут быть получены как скалярное произведение векторов:
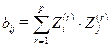 (4.4.9)
(4.4.9)
6. Неметрические методы МНШ.
В неметрическом многомерном шкалировании предполагается, что различие между объектами измерено в рангах.
Процедура неметрического МНШ строится так, чтобы ранговый порядок попарных расстояний между точками минимально отличался от того, который задан.
Для определения меры соответствия Дж.Красколон предложил следующий критерий, названный им «стресс»
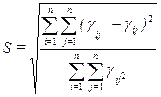 , (4.6.1)
, (4.6.1)
Где 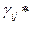 - расстояние между объектами в р-мерном пространстве.
- расстояние между объектами в р-мерном пространстве.
Можно использовать также критерий:
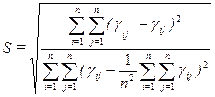 (4.6.2)
(4.6.2)
Л. Гуттманом предложен критерий, который назван коэффициентом отчуждения. Для расчета последнего рассчитывается коэффициент монотонности
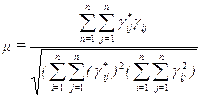 (4.6.3)
(4.6.3)
Коэффициент монотонности является ранговой мерой согласованности, указывающей степень порядковой связи между исходными данными и оценками расстояний. Зная коэффициент монотонности, можно определить коэффициент отчуждения:
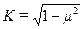 .
.
Алгоритм МНШ:
1. Интеграция k=0
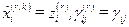 , i,j = 1,…,n, r=1,…,р
, i,j = 1,…,n, r=1,…,р
Текущее значение стресс - критерия S=0.
2.Нормирование:
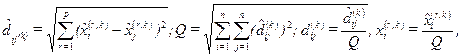 i,j = 1,…,n
i,j = 1,…,n
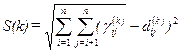
3.Если k>0 и 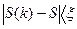 , где ξ – требуемая точность вычислений, расчет закончен. Если – нет, то полагаем S=S(k) и процедура продолжается с шага 4.
, где ξ – требуемая точность вычислений, расчет закончен. Если – нет, то полагаем S=S(k) и процедура продолжается с шага 4.
4.Упорядование.
Выполняется при k=0. упорядочить пары (i,j) по возрастанию различий 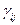 . Если для некоторых пар
. Если для некоторых пар 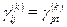 и
и 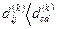 то пары i,j должны предшествовать (c,d). Если равны и различия и расстояния, то порядок пар произвольный. В результате получим таблицу из
то пары i,j должны предшествовать (c,d). Если равны и различия и расстояния, то порядок пар произвольный. В результате получим таблицу из 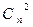 строк и трех столбцов. В первом – обозначены пары, во втором – различия для пар объектов в порядке возрастания, в третьем – расстояния между объектами. Процедура продолжается пока расстояния не окажутся упорядоченными.
строк и трех столбцов. В первом – обозначены пары, во втором – различия для пар объектов в порядке возрастания, в третьем – расстояния между объектами. Процедура продолжается пока расстояния не окажутся упорядоченными.
5.Если соседние в таблице числа 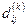 имеют равные величины, то соответствующие им пары индексов объединяют в блок. Если равных расстояний нет, то каждую пару считают самостоятельным блоком.
имеют равные величины, то соответствующие им пары индексов объединяют в блок. Если равных расстояний нет, то каждую пару считают самостоятельным блоком.
6. Определяется число блоков. Пусть их m 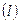 и каждому s-му блоку соответствует расстояние d(s), s=
и каждому s-му блоку соответствует расстояние d(s), s= 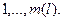 Положим s=1.
Положим s=1.
7.Сравним s-й и (s+1)-й блоки. Если d(s)<d(s+1), то переходим к шагу 8. Если – нет, то объединяем эти блоки в один и присваиваем ему номер s+1. Для него d(s+1)= 1/2(d(s)+d(s+1)).
8.Полагаем s=s+1. Если s< 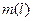 , то переход к шагу 7. Если нет – то переход к шагу 9.
, то переход к шагу 7. Если нет – то переход к шагу 9.
9. Если на шаге 7 объединялись какие-либо блоки, то 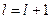 и к шагу 6, иначе к шагу 10.
и к шагу 6, иначе к шагу 10.
10.Пересчитаем координаты 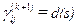 при (i,j) в s-ом блоке, s=
при (i,j) в s-ом блоке, s= 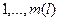 и по формуле Дж.Лингоса и Э.Росмана
и по формуле Дж.Лингоса и Э.Росмана 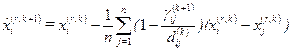 , i=1,…,n, r=1,…,p.
, i=1,…,n, r=1,…,p.
Если 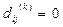 , то отношение
, то отношение 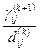 полагают равным 1.
полагают равным 1.
Увеличиваем k: k=k+1. Переходим к шагу 2.
В результате работы алгоритма получаем числа 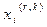 , i=1,….,n, r=1,…, p, которые суть наилучшие оценки координат изучаемых оценок в p – мерном пространстве с заданной точностью.
, i=1,….,n, r=1,…, p, которые суть наилучшие оценки координат изучаемых оценок в p – мерном пространстве с заданной точностью.
Шаги 3-9 называются неметрическим этапом алгоритма Торгерсона. Шаг 10 алгоритма называется метрическим этапом. Формулы пересчета координат выписаны из условия уменьшения величины стресса.
7. Кластерный анализ.
Классификация объектов по осмысленным группам, называется кластеризацией, является важной процедурой в различных областях научных исследований. Кластерный анализ (КА) – это многомерная статистическая процедура, упорядочивающая исходные данные (объекты) в сравнительно однородные группы. Общим для всех исследований, использующих КА, являются пять основных процедур: 1) отбор выборки для кластеризации; 2) определение множества признаков, по которым будут оцениваться объекты в выборке; 3) вычисление значений той или иной меры сходства между объектами; 4) применение метода КА для создания групп исходных данных; 5) проверка достоверности результатов кластерного решения.
Каждый из перечисленных шагов играет существенную роль при использовании КА в прикладном анализе данных. При этом шаги 1,2,5 целиком зависят от решаемой задачи и должны определяться пользователем. Шаги 3 и 4 выполняются программой КА.
В целом многие методы КА – довольно простые эвристические процедуры, которые не имеют, как правило, строгого статистического обоснования, но позволяют свести к минимуму вероятность допущения ошибки при трактовке результатов КА.
Разные кластерные методы могут порождать различные решения для одних и тех же данных. Это обычное явление в большинстве прикладных исследований. Окончательным критерием считают удовлетворенность исследователя результатами КА,
Разработанные кластерные методы образуют семь основных семейств: иерархические агломеративные методы; иерархические дивизимные методы; итеративные методы группировки; методы поиска модальных значений плотности; факторные методы; методы сгущений; методы использующие теорию графов.
По данным ряда исследований, около 2/3 приложений КА используют иерархические агломеративные методы. Рассмотрим его сущность на примере наиболее простого метода одиночной связи.
Процесс кластеризации начинается с поиска двух самых близких объектов в матрице расстояний. На последующих шагах к этой группе присоединяется объект, наиболее близкий к одному из уже находящихся группе. По окончании кластеризации все объекты объединяются в один кластер.
Отметим несколько важных особенностей иерархических агломеративных методов: 1) все эти методы просматривают матрицу расстояний размерностью N×N (где N – число объектов) и последовательность объединения кластеров можно представить визуально в виде древовидной диаграммы, часто называемой дендрограммой; 3) для понимания этого класса методов не нужны обширные знания матричной алгебры или математической статистики. Вместо этого дается правило объединения объектов в кластеры.
Математически формализованная процедура разбиения анализируемой совокупности объектов О1, О2, …, Оn на некоторое число однородных в определенном классе в условиях отсутствия обобщающих выборок. При этом исходная информация представляется либо значениями многомерного признака (по каждому объекту в отдельности), либо матрицей попарных расстояний (или близостей) между объектами. Понятие однородности основано на предположении, что геометрическая близость двух или нескольких объектов означает близость их «физических» состояний, их сходство. Полученные в результате разбиения классы часто называют кластерами (токсонами, образами), а методы их нахождения соответственно кластер – численной токсономией, распознаванием образов с самообучением.
Математическая постановка задачи требует формализации понятия «качество разбиения». С этой целью вводится понятие критерия (функционала) качества разбиения Q(S), который задает способ сопоставления с каждым возможным разбиением S заданного множества объектов на классы некоторого числа Q(S), оценивающего (в определенной шкале) степень оптимальности данного разбиения. Тогда задача поиска наилучшего разбиения S* сводится к решению оптимизационной задачи:
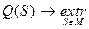 , (4.7.1)
, (4.7.1)
где М – множество всех допустимых разбиений.
В статистической практике выбор функционала качества разбиения Q(S) обычно осуществляется произвольно, опирается скорее на эмпирические и профессионально-интуитивные соображения, чем на какую-либо точную формализованную схему. Однако ряд распространенных в статистической практике функционалов качества удается обосновать в рамках строгих математических моделей. Возможность этого появляется при наличии дополнительных априорных сведений о классах, позволяющих, например, представлять каждый класс в качестве параметрически заданной генеральной совокупности. Известен также метод, представленный аппроксимационными моделями, когда искомая классификация характеризуется матрицей определенной структуры (например, аддитивными кластерами). Задача состоит в том, чтобы оценить параметры этой структуры таким образом, чтобы она минимально отличалась от матрицы исходных данных. В такой постановке проблема классификации сближается с проблемами факторного анализа. В теории и практике статистического анализа данных широко известны следующие методы кластер-анализа: ФОРЕЛЬ, К-средних (Мак-Кунна), ИСОМАД, метод динамических сгущений, ближайшего соседа.
На результаты кластеризации существенное влияние оказывает выбор меры расстояния. На практике их лучше бы называть мерами несходства: для большинства используемых коэффициентов большие значения соответствуют большему сходству, в то время как для мер расстояний все наоборот. Считается, что два объекта идентичны, если описывающие их переменные принимают одинаковые значения. В этом случае расстояние между ними равно нулю. Меры расстояния обычно не ограничены сверху и зависят от выбора шкалы (масштаба) измерения. В программе кластеризации проводится на основе метрик: евклидово расстояние; корреляционное расстояние; расстояние городских кварталов (манхеттенское); расстояние Махаланобиса (обобщенное расстояние); вычисляемых по формулам в таблице 4.7.1.
Таблица 4.7.1. – Расчетные формулы метрик кластеризации
| № | Показатель | Формула расчета |
| Евклидово расстояние |  | |
| Корреляционное расстояние | 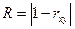 | |
| Расстояние городских кварталов | 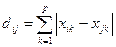 | |
| Расстояние Махаланобиса | 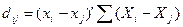 |
Главным недостатком коэффициента корреляции как меры сходства является его чувствительность к форме при сниженной чувствительности к величине различий между переменными. Он также часто не удовлетворяет неравенству треугольника, и корреляция, вычмсленная этим способом, не имеет статистического смысла, так как среднее значение определяется по совокупности всевозможных разнотипных переменных, а не по совокупности объектов (смысл «среднего» по разнотипным переменным далеко не ясен). Однако данный коэффициент широко используется в приложениях кластерного анализа.
Несмотря на важность евклидовой и других метрик, они имеют серьезные недостатки. Наиболее важный состоит в том, что оценка сходства сильно зависти от различий в сдвигах данных. Переменные у которых одновременно велики абсолютные значения и стандартные отклонения, могут подавить влияние переменных с меньшими абсолютными размерами и стандартными отклонениями. Более того, метрические расстояния изменяются под воздействием преобразованной шкалы измерения переменных, при которых не сохраняется ранжирование по евклидову расстоянию. Чтобы уменьшить влияние относительных величин переменных, обычно перед вычислением расстояния переменные нормируют к единой дисперсии и нулевому среднему.
В отличие от евклидовой и других аналогичных метрик метрика расстояния Махаланобиса с помощью матрицы дисперсий – ковариаций связана с корреляциями переменных. Когда корреляция между переменными равно нулю, расстояние Махаланобиса эквивалентно квадратичному евклидову расстоянию.
Для графической интерпретации результатов кластерного анализа проводится график расположения исходных объектов в пространстве первых двух главных компонент. При этом объекты, попавшие в один кластер, отображаются одним цветом. Иногда объекты из разных кластеров расположены столь близко, что может создаться иллюзия неправильной классификации. Это связано с тем, что классификация проводится по большому числу переменных, а график строится по двум координатам, хотя и отражающим основные особенности данных, поэтому расхождения между результатом классификации и графическим отображением неизбежны.
8. Дискриминантный анализ
Дискриминантный анализ предназначен для решения задач, связанных с разделением на классы совокупностей наблюдений.
Пусть имеются исходные данные, подлежащие классификации наблюдения в виде матрицы данных х. Причем, предполагается, что они представляют выборку из генеральной совокупности, являющейся смесью наблюдений из k классов D1, D2, …, Dk. При этом i-му классу соответствует закон распределения вероятностей Pi(x), i=1,2, …, k. Априорное описание классов заключается в том, что распределение Pi(x) либо известны, либо статистически могут быть оценены по имеющимся в распоряжении обучающим выборкам xji Î Dj. (Выборка называется обучающей, если известно, что все ее наблюдения xi извлечены из одной и той же генеральной совокупности Dj). Требуется указать правило классификации S, относящее наблюдения из х к одному из классов (законов распределения) Dj с минимальными, в определенном смысле потерями. Обучающие выборки могут составлять часть выборки х.
Общий вид функции качества классификации определяется в виде:
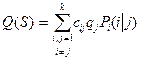 (4.8.1)
(4.8.1)
где: сij – потери от классификации объекта из j-го класса в i-ый класс;
qj – удельный вес (априорная вероятность) объектов j-го класса;
Рi(i|j) –вероятность ошибочной классификации объектов j-го класса в i-й класс при использовании классификационного правила S’.
Во многих реальных задачах трудно оценить потери сij из-за неправильной классификации объектов, а иногда и априорной вероятности qj появления объектов различных классов. Для этих случаев используется специальные подходы.
К понятию дискриминантного анализа можно отнести задачи по разделению множества объектов на два непересекающихся класса. Множество объектов может представляться группой предприятий, характеризующихся одинаковыми показателями производственно-финансовой деятельности. Это могут быть сельскохозяйственные предприятия, заводы, фабрики, банки и т.д., среди которых нужно выделить класс эффективно функционирующих и класс объектов неэффективно функционирующих. Это могут быть группы семей, которые обследуются по качеству жилищных условий, которые характеризуются несколькими показателями, это могут быть группы животных, продуктивность которых и племенные особенности характеризуются многими показателями. Результаты решения выше указанных задач с успехом могут быть использованы в принятии управленческих решений. Например, в решении вопроса о закрытии класса неэффективно функционирующих предприятий или предоставления кредитных ресурсов эффективно работающим предприятиям, а также для уточнения решения экспертных оценок, т.е. проверить гипотезу о верности экспертного заключения.
Каждый объект в дальнейшем обозначим m-мерным вектором, координаты которого определяют значения показателей, характеризующих объект, тогда можно сформулировать задачу следующим образом.
ПОСТАНОВКА ЗАДАЧИ.
В m-мерном векторном пространстве заданы n векторов:
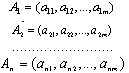
Требуется проверить статистическую гипотезу о возможности разбиения n-объектов на два непересекающихся класса с заданным уровнем значимости.
Исходные данные (входная информация) задается в виде матрицы:
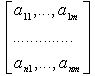
Теоретической основой метода дискриминантного анализа является регрессионный анализ, сущность которого сводится к построению следующей многофакторной линейной функции регрессии, называемой иначе дискриминирующей:
y = a0 + a1x1 + a2x2 +... + amxm,
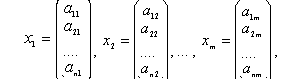 где:
где: 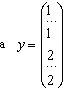
количество единиц в матрице-столбце у определяет количество объектов, относящихся к первому классу, а количество двоек – количество объектов относящихся ко второму классу.
Для расчета коэффициентов функции регрессии используется метод наименьших квадратов, т.е. составляется функция
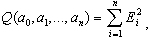
которая суммирует квадраты отклонения эмпирических от теоретических результативных признаков:
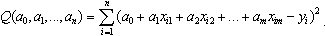
Коэффициенты дискриминирующей функции можно найти, решив систему уравнений:
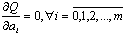
При нахождении коэффициентов дискриминирующей функции возникают затруднения вычислительного характера, связанные с нахождением определителей высокого порядка, поэтому для вычисления коэффициентов дискриминирующей функции нужно использовать программу «Дискриминантный анализ» из ППП “STADIA”.
При этом нужно учитывать следующие особенности:
1) Число объектов относящихся априорно к первому классу в матрице исходных данных нужно записывать первыми.
2) Необходимо указать в ходе расчетов априорные вероятности отнесения объектов к первому и второму классу, в частности, при разбиении на равные по количеству объектов классы, (исходно обе вероятности равны 0,5) при неравных по числу классам вычисляются по формулам: 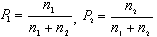 (4.8.2)
(4.8.2)
где: n1 - число объектов, априорно относимых к первому классу; n2 - число объектов, априорно относимых ко второму классу.
3) Нужно указать стоимости (или штрафы, выраженные в произвольных единицах) ошибочной классификации, т.е. отнесения объекта из первого класса ко второму классу и наоборот из второго к первому.
Расчеты производятся в следующем порядке:
1. Находится функция регрессии, которую принято называть, в данном случае, дискриминирующей функцией.
2. Находится коэффициент корреляции.
3. Определяется расстояние Мехаланобиса, отражающее степень разделения двух классов объектов по формуле:
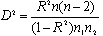 (4.8.3)
(4.8.3)
4.Приведенное или несмешанное расстояние:
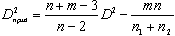 (4.8.4)
(4.8.4)
5.Вычисляется значение F-статистики Фишера:
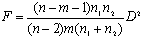 (4.8.5)
(4.8.5)
и вероятность Р нулевой гипотезы о незначительности классификации (т.е. о том, что расстояние между классами равно нулю).
1. Находятся апостериорные вероятности правильной классификации:
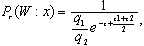 (4.8.6)
(4.8.6)
где: q1 и q
|
|
 2015-10-13
2015-10-13 1462
1462
