2015-10-13
448
Большое значение для построения подходящей статистики имеет факт применимости закона больших чисел к эмпирической функции распределения, Именно, имеет место следующая теорема.
Теорема 5.4.1. Пусть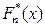 
- эмпирическая функция распределения, построенная по выборке 
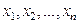из генеральной совокупности 
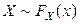. Тогда для 
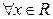и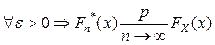 
.
Имеем по определению: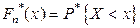 
, т.е. при каждом действительном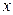 
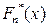есть относительная частота события 
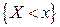(«успеха») в n опытах по схеме Бернулли с вероятностью «успеха» 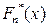. Поэтому утверждение теоремы следует из ЗБЧ в формулировке Бернулли. 
Колмогоровым была изучена статистика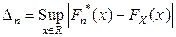 
- точная верхняя грань отклонения эмпирической функции распределения от теоретической на всей оси, - и на ее основе разработан критерий согласия. Имеет место следующая теорема:
Теорема 5.4.2 (Колмогоров). Пусть Х -СВНТ с функцией распределения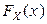 
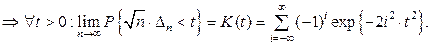
без доказательства [ см. например, [5], §3.2]
Функция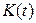 
- функция распределения Колмогорова – табулирована и может быть использована для проверки гипотезы о законе распределения непрерывной генеральной случайной величины с помощью статистики 
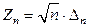уже при 
.
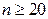На практике экстремум заменяется на максимум, который достигается в одной из точек скачка эмпирической функции распределения (если она строится для простой выборки). Несколько сложнее осуществляется поиск максимума отклонения для интервальной выборки. При этом возникает не простой вопрос о зависимости мощности критерия от числа интервалов, если эти интервалы не порождены естественной классификацией признаков в номинальной шкале.
