Критерий хи-квадрат более алгоритмичен, чем критерий Колмогорова, и имеет более широкий спектр приложений, т.к. применяется как для дискретной так и непрерывной генеральной совокупности. Основан этот критерий на поразрядном сравнении частот и вероятностей, поэтому предварительно выборка приводится к частотному виду. При этом в зависимости от типа генерального по разному трактуется понятие «разряд». Именно:
Если генеральная 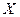 является СВДТ, то разрядами являются возможные значения
является СВДТ, то разрядами являются возможные значения 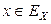 в группированной выборке.
в группированной выборке.
Если же генеральная 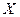 является СВНТ, то разрядами являются интервалы при интервальном представлении выборки.
является СВНТ, то разрядами являются интервалы при интервальном представлении выборки.
Рассмотрим более подробно структуру критерия для непрерывной Х. Пусть гипотеза  – простая, т.е. полностью определяет закон распределения X.
– простая, т.е. полностью определяет закон распределения X.
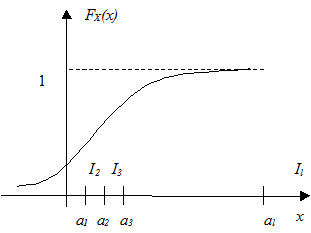 | Разобьем множество значений 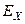 на на 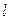 интервалов точками деления интервалов точками деления 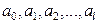 , как показано на рисунке, так что , как показано на рисунке, так что 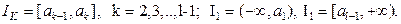 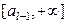 |
Т.к.  – простая, то теоретическая вероятность попадания на интервал
– простая, то теоретическая вероятность попадания на интервал 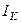 :
: 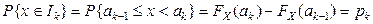 - точно иизвестна.
- точно иизвестна.
Пусть получена выборка: 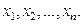 Распределим ее по интервалам: пусть
Распределим ее по интервалам: пусть 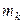 - число выборочных значений, попавших в
- число выборочных значений, попавших в 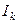 .
.
Очевидно должно выполнятся условие: 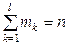 (5.4.1)
(5.4.1)
Рассмотрим меру расхождения, основанную на среднеквадратичной близости:
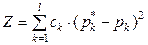 , где
, где 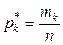 . Имеет место следующая теорема.
. Имеет место следующая теорема.
Теорема 5.4. 3. (Пирсон) Если  – простая,
– простая, 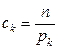 ,
, 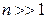 , то
, то
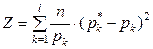 ~
~ 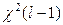
 Преобразуем:
Преобразуем: 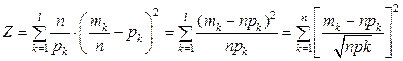 .
.
Обозначим: 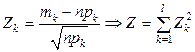 (5.4.2)
(5.4.2)
Можно показать, что при больших n 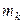 ~
~ 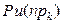 , т.е. Zk – стандартизованная пуассоновская величина.
, т.е. Zk – стандартизованная пуассоновская величина.
Известно, что пуассоновское распределение асимптотически нормально
(см. задачу 18.572 в [1]). Поэтому при 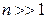 таких, что
таких, что 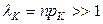 для всех
для всех 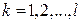 можно считать, что
можно считать, что 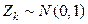 . Отсюда согласно (5.4.2), статистика Z представляет собой сумму квадратов стандартизированных нормальных величин. Если бы
. Отсюда согласно (5.4.2), статистика Z представляет собой сумму квадратов стандартизированных нормальных величин. Если бы 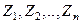 были независимы в совокупности, то в соответствии с теоремой Пирсона можно было утверждать, что
были независимы в совокупности, то в соответствии с теоремой Пирсона можно было утверждать, что 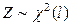 . Однако утверждение о независимости в данном случае не имеет места, т.к. на случайные величины
. Однако утверждение о независимости в данном случае не имеет места, т.к. на случайные величины 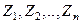 наложено одно линейное условие связи. Действительно, как следует из (5.4.2):
наложено одно линейное условие связи. Действительно, как следует из (5.4.2): 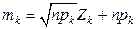 .
.
Учитывая условие (5.4.1), получаем:
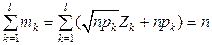
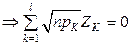 - линейная зависимость между величинами
- линейная зависимость между величинами 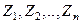 . При этом, согласно основной концепции распределения хи-квадрат, «теряется одна степень свободы», и в результате получаем:
. При этом, согласно основной концепции распределения хи-квадрат, «теряется одна степень свободы», и в результате получаем:
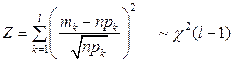 , (5.4.3)
, (5.4.3)
что и требовалось доказать. 
Замечание 1. Критическую область для проверки основной гипотезы  следует выбирать на правом хвосте распределения
следует выбирать на правом хвосте распределения 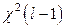 , т.к. это максимизирует мощность критерия. Действительно, если гипотеза
, т.к. это максимизирует мощность критерия. Действительно, если гипотеза  - ложная, т.е.
- ложная, т.е. 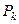 не являются истинными вероятностными k- го разряда, то каждое слагаемое в сумме (5.4.2) будет иметь порядок n и сумма будет неограниченно возрастать вместе с объемом выборки. Таким образом, если
не являются истинными вероятностными k- го разряда, то каждое слагаемое в сумме (5.4.2) будет иметь порядок n и сумма будет неограниченно возрастать вместе с объемом выборки. Таким образом, если 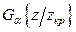 , то при достаточно большом n событие
, то при достаточно большом n событие 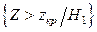 будет иметь вероятность, близкую к единице, и ложная гипотеза будет почти наверняка отвергнута.
будет иметь вероятность, близкую к единице, и ложная гипотеза будет почти наверняка отвергнута.
Пример 5.4.1. Исследуя вероятностные законы наследственности, Грегор Мендель проводил в течение 8 лет (с 1857 по 1865г.) эксперименты по селекции гороха. За это время он вырастил и детально изучил около 10000 растений гороха, прежде чем решился опубликовать свои результаты в одном из научных журналов. Однако после этого события потребовалось 35 лет для того, чтобы ученый мир понял и оценил значение сделанного им открытия. В одном из своих экспериментов Мендель наблюдал частоты различных видов семян, получаемых при скрещивании растений с круглыми желтыми семенами и растений с морщинистыми зелеными семенами. Эти данные наблюдений и теоретически рассчитанные вероятности приведены в следующей таблице:
| Номер разряда | Виды семян | Частота 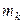 | Теоретические вероятности 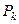 |
| 1. | Круглые и желтые | 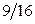 | |
| 2. | Морщинистые и желтые | 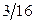 | |
| 3. | Круглые и зеленые | 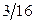 | |
| 4. | Морщинистые и зеленые | 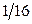 |
Проверить на уровне значимости 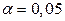 основную гипотезу о соответствии наблюдаемых частот теоретическим вероятностям.
основную гипотезу о соответствии наблюдаемых частот теоретическим вероятностям.
 В данном примере разрядами являются значения качественных признаков:
В данном примере разрядами являются значения качественных признаков: 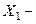 форма (круглые или морщинистые),
форма (круглые или морщинистые), 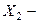 цвет (желтый или зеленый), по которым вся популяция гороха (генеральная совокупность) разделилась на 4 непересекающихся класса. Статистика Пирсона принимает вид:
цвет (желтый или зеленый), по которым вся популяция гороха (генеральная совокупность) разделилась на 4 непересекающихся класса. Статистика Пирсона принимает вид:
 .
.
Из таблицы квантилей распределения 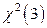 находим:
находим: 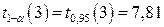 . Вычисляем выборочное значение статистики:
. Вычисляем выборочное значение статистики: 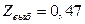 . Так как 0,47<<7,81 (
. Так как 0,47<<7,81 (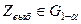 ) то гипотеза
) то гипотеза  принимается с хорошей надежностью.
принимается с хорошей надежностью. 
Замечание 2. Выбор интервалов – не простая задача при практическом использовании критерия хи-квадрат. Следует иметь в виду, что преобразование выборки к интервальному виду (в случае непрерывной Х) связано с некоторой потерей информации. Однако для эффективной работы критерия Пирсона группировка является необходимой операцией, позволяющей параметризировать критерий. Но при этом число интервалов 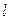 не должно быть ни слишком малым, иначе будет потерянно слишком много информации о распределении генеральной совокупности, ни слишком большим, т.к. в этом случае получаются слабо наполненные разряды, и мощность критерия падает. Теоретически этот вопрос исследовался в специальной литературе, где было показано, что при проверке на нормальность оптимальное число интервалов группировки определятся соотношением
не должно быть ни слишком малым, иначе будет потерянно слишком много информации о распределении генеральной совокупности, ни слишком большим, т.к. в этом случае получаются слабо наполненные разряды, и мощность критерия падает. Теоретически этот вопрос исследовался в специальной литературе, где было показано, что при проверке на нормальность оптимальное число интервалов группировки определятся соотношением
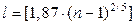 ,
,
(где [a] – целая часть числа a), которое может служить ориентиром и для проверки других типов распределений, отличных от нормального.
Замечание 3. Обобщение критерия на случай сложной гипотезы.
Пусть гипотеза  - сложная, т.е. гипотетическая функция распределения
- сложная, т.е. гипотетическая функция распределения 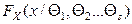 зависит от
зависит от 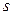 неизвестных параметров. В этом случае теоретические вероятности
неизвестных параметров. В этом случае теоретические вероятности 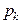 попадания на интервал
попадания на интервал 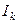 при условии
при условии  не могут быть вычислены точно, т.к. они сами являются функциями этих неизвестных параметров:
не могут быть вычислены точно, т.к. они сами являются функциями этих неизвестных параметров:
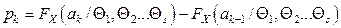 .
.
Необходимо оценить значения параметров 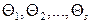 по выборке, что приведет к оценкам теоретических вероятностей
по выборке, что приведет к оценкам теоретических вероятностей 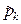 вместо точных значений
вместо точных значений 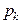 . Возникает вопрос: как это повлияет на закон распределения статистики Z? Как доказано Фишером, если параметры оцениваются методом максимального правдоподобия для интервальной выборки, то при достаточно больших n получим:
. Возникает вопрос: как это повлияет на закон распределения статистики Z? Как доказано Фишером, если параметры оцениваются методом максимального правдоподобия для интервальной выборки, то при достаточно больших n получим: 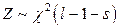 , т.е. снова получаем распределение хи-квадрат, но теряем дополнительно s степеней свободы по числу оцениваемых параметров.
, т.е. снова получаем распределение хи-квадрат, но теряем дополнительно s степеней свободы по числу оцениваемых параметров.
Пример 5.4.2. Для проверки на равномерность распределения последовательности псевдослучайных чисел, вырабатываемых генератором (команда rand в пакете MATLAB), взято 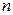 =2000 таких чисел и рассортировано по десяти интервалам равной длины
=2000 таких чисел и рассортировано по десяти интервалам равной длины 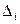 =0,1;
=0,1; 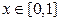 . Получен следующий статистический ряд в интервальном представлении:
. Получен следующий статистический ряд в интервальном представлении:
| Номер интервала | ||||||||||
| Число попаданий |
На уровне значимости  =0,05 проверить основную гипотезу
=0,05 проверить основную гипотезу  , утверждающую, что данная выборка принадлежит генеральной совокупности
, утверждающую, что данная выборка принадлежит генеральной совокупности 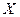 , распределенной по закону
, распределенной по закону 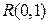 .
.
◄ В нашем случае число интервалов группировки 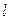 =10. Гипотеза
=10. Гипотеза  - простая, поэтому согласно теории статистика Пирсона
- простая, поэтому согласно теории статистика Пирсона 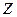 распределена по закону
распределена по закону 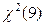 . Критическая область определяется условием
. Критическая область определяется условием 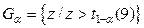 , где
, где
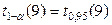 =16,9 – из таблицы квантилей распределения хи-квадрат. Теоретическое число попаданий на интервал
=16,9 – из таблицы квантилей распределения хи-квадрат. Теоретическое число попаданий на интервал 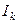 при условии справедливости гипотезы
при условии справедливости гипотезы  равно
равно 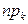 =2000
=2000 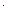 0,1=200,
0,1=200, 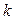 =1,2,…,10.
=1,2,…,10.
Выборочное значение статистики вычисляем по формуле (5.4.3): 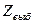 =5,3. Т.к.
=5,3. Т.к. 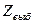
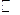 16,9, то выборочные данные хорошо согласуются с гипотезой
16,9, то выборочные данные хорошо согласуются с гипотезой  .►
.►
Замечание 4. Рассмотренные в настоящем параграфе две задачи преследовали лишь цель продемонстрировать методику решения задачи проверки гипотез о законе распределения. Большинство задач такого рода (например, проверка на нормальность) требуют проведения больших вычислений, поэтому их рекомендуется выполнять в рамках лабораторных работ.
Контрольные вопросы к главе 5
1. Что называется параметрической гипотезой?
2. Дать определение простой и сложной гипотезы.
3. Написать уравнение, определяющее вероятность ошибки первого рода.
4. Написать уравнение, определяющее вероятность ошибки второго рода.
5. Как ставится задача выбора критической области?
6. Сформулировать решающее правило проверки основной гипотезы.
7. Что такое мощность правила?
8. Выписать подходящую статистику для проверки основной гипотезы о равенстве дисперсии эталонному значению (при известном и неизвестном матожидании).
9. Выписать подходящую статистику для проверки основной гипотезы о равенстве матожидания эталонному значению (при известной и неизвестной дисперсии).
10. Выписать подходящую статистику для проверки основной гипотезы о равенстве дисперсий (при известных и неизвестных матожиданиях).
11. Выписать подходящую статистику для проверки основной гипотезы о равенстве матожиданий (при известных и неизвестных дисперсиях).
12. Записать оценку дисперсии объединенной выборки. Указать свойства этой оценки.
13. Выписать подходящую статистику для проверки основной гипотезы о равенстве вероятностей. Каков закон распределения этой статистики?
14. Как ставится задача проверки гипотезы о законе распределения?
15. Написать выражение для статистики Пирсона и определить смысл всех входящих в нее величин. Каков закон распределения этой статистики в случае простой гипотезы?
16. Чем определяется высокая мощность критерия Пирсона?
17. Как осуществляется выбор интервалов группировки при использовании критерия Пирсона?
18. Что меняется в критерии Пирсона, если  - сложная гипотеза?
- сложная гипотеза?
 2015-10-13
2015-10-13 2248
2248