Проверка гипотез о сравнении характеристик в двух независимых генеральных

Сравнение дисперсий.

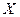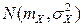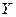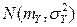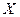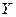Постановка задачи. Пусть ~ , ~ причем и – независимы (параметры 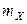и 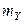могут быть известны или неизвестны).

Из этих совокупностей взяты выборк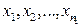и

, и 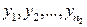, после обработки которых получены соответствующие оценк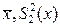и и .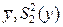

При заданном уровне значимости проверяется основная гипотеза

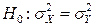
против одной из альтернатив

.

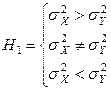Как следует из общей схемы проверки гипотез, необходимо иметь подходящую статистику, удовлетворяющую двум обязательным условиям:

1) быть подходящей мерой расхождения между гипотетическим значением, утверждаемым в , и соответствующим выборочным значением;

2) Закон распределения этой статистики должен быть полностью определен по крайней мере при условии . Структура этой статистики должна быть такова, чтобы можно было вычислить выборочное значение 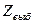(статистика не должна содержать мешающих параметров).Другими словами, гипотеза должна быть простой.

Такую статистику для данной постановки задачи можно построить на основе выборочных несмещенных оценок дисперсии для обеих совокупностей.

Пример 5.3.1. Показать, что при условиях, наложенных на генеральные совокупности статистика:

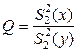при условии подчиняется закону Фишера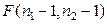

◄ Составим две известные статистик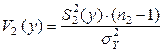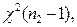и:

~ и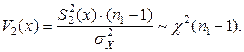

(эти выборочные статистики изучены в 4.4)

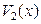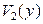Ясно, что и независимы. Þ по теореме Фишера (см. (4.5.8)) имеем:

~ .

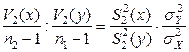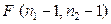При условии дисперсии в выражении для 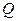сокращаются. Þполучаем требуемый результат.

Замечание 1. Критическая область для проверки гипотезы выбирается в соответствии с правилами оптимизации ошибок I и II рода для несимметричных распределений. При этом следует учитывать, что в таблице квантилей распределения Фишера приводятся лишь значения > 1. Чтобы получить значения квантили, меньшее единицы (это необходимо, например, при использовании левосторонней альтернативы), следует использовать следующее соотношение между квантилиями, вытекающее из свойств фишеровского распределения (4.4.6):

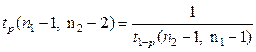
Замечание 2. Если в постановке задачи математические ожидания 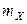и и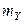звестны, то следует использовать статистику ~

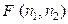
Сравнение средних (математических ожиданий).

Пусть две генеральные X и Y удовлетворяют тем же условиям, что и при сравнении дисперсий. Проверяются основная гипотеза 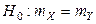против одной из альтернатив:

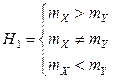
Рассмотрим два случая.

Случай 1. 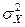и и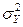звестны. -

Пример 5.3.2.. Показать, что подходящей статистикой для проверки основной гипотезы в данном случае является статистика

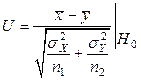~ N (0,1)

Рассмотрим статистику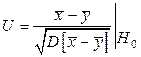

Тот факт, что 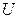является подходящей мерой расхождения, очевидно по ее построению. Таким образом, условие 1) выполняется. Проверим условие 2). Заметим, что вывод закона распределения этой статистики изучен в 4.4 (см. равенство (4.5.9)). Из методических соображений мы повторим некоторые детали доказательства применительно к данной постановке задачи.

Поскольку U является стандартизированной линейной комбинацией независимых нормальных случайных величин, то очевидно, что U распределена нормально. Вычислим основные характеристики M [ U ] и D[ U ] в предположении, что верна. Используя свойства операторов матожидания и дисперсии, получаем:

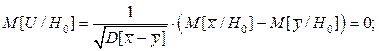
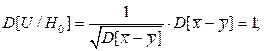
Далее имеем:

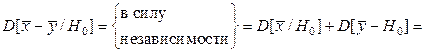
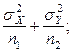
Таким образом,

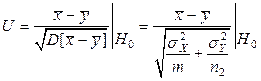~ N (0,1).

Тем самым установлено выполнение условия 2)

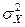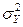Случай 2. и - неизвестны. В этом случае статистику U, определенную в примере 5.2.2., использовать нельзя. Гипотеза о равенстве маетматических ожиданий проверяется в 2 этапа. На первом этапе необходимо проверить вспомогательную гипотезу 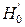о равенстве дисперсий. При этом в качестве альтернативы используется как правило двусторонняя или такая, которая подсказана опытными данными.

Далее возможны два случая.

Случай 2.1 Дисперсии неизвестны, но подтверждается гипотеза об их равенстве.

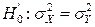- подтверждается на том же уровне a.

Случай 2.2. Гипотеза 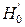отклоняется.

Рассмотрим случай 2.1.

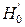
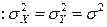- В этом случае статистику 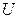можно записать так:

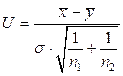~ N (0,1),

но так как точное значение дисперсии неизвестно, то 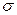- мешающий параметр.

Пример 5.3.3. Обозначим

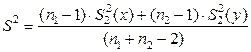(5.3.1)

так называемая несмещенная выборочная дисперсия объединенной выборки.

Покажем, что статистика 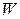, определяемая равенством

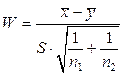
является подходящей статистикой для проверки основной гипотезы .

Заметим, что 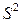является состоятельной и более эффективной оценкой неизвестной дисперии 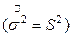, чем несмещенные оценки того же параметра, полученные для каждой из выборок в отдельности (см. параграф 4.4).

Закон распределения статистики 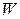изучен в 4.4, где показано, что при условии 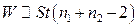. При этом 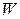не содержит мешающих параметров. Таким образом, снова выполняется условие 2) подходящей статистики ►

Случай 2.2.

Вспомогательная гипотеза 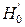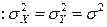- отклоняется на данном уровне значимости a Þ статистика W – неприменима Þ используется так называемая статистика Уэлча:

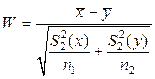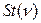~ , где 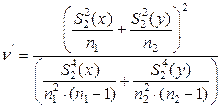(5.3.2)

.

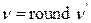Это утверждение мы примем без доказательства ввиду его сложности.

Сравнение вероятностей.

Пусть генеральные X и Y представляют собой два индикатора:

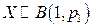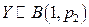, . Проверяется основная гипотеза о равенстве вероятностей:

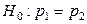
против одной из альтернатив:

Взяты две выборки соответственно из 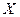и 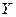и для каждой из них вычислены относительные частоты как оценки неизвестных вероятностей

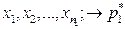- относительная частота: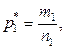

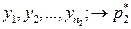- относительная частота: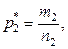

где 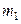и 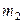–число единиц в соответствующих выборках.

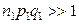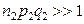Пример 5.3.4. Покажем, что при условиях и подходящей статистикой для проверки основной гипотезы является статистика

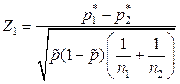, где 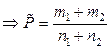- оценка неизвестной вероятности по объединенной выборке.

Подходящей мерой расхождения является статистика, структура которой определяется формулой

:

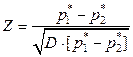
Проверим выполнение условия 2).

Так как Z – стандартизованная линейная форма, а 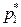и 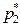- асимптотически нормальны по теореме Муавра-Лапласа, то распределение Z – асимптотически нормально. Остается проверить характеристики и упростить выражение для Z. Для этого вычислим M [ Z ] и D [ Z ] в предположении, что справедлива :

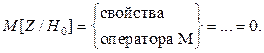
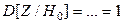. Далее, учитывая, что свойства относительной частоты нам хорошо известны, получаем:

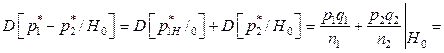
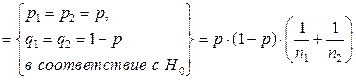, где р – неизвестная вероятность – общая для обеих генеральных Þ cтатистика: 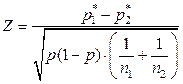при условии распределена по закону N (0,1) при одновременном выполнении условий: 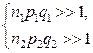(5.3.3)

Неизвестное значение вероятности р оценивается по объединенной выборке:

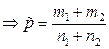и при условиях (5.3.3) при подстановке в 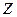не изменяют закон распределения.

Таким образом, окончательно статистика Z приобретает вид: .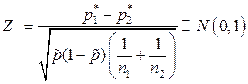

Пример 5.3.5. В двух фирмах, производящих детское питание, производилась оценка какчества продукции. В фирме 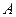, где проверялось 30 единиц продукции, средняя сумма баллов оказалась равной 52. Во второй фирме 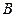проверялось 36 единиц продукции, и их средняя сумма баллов оказалась равной 45. Средние квадратичные отклонения суммы баллов, вычисленные для нескольких тысяч единиц продукции каждой из фирм, равны: 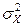=15 для фирмы 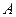и 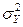=12 для фирмы 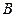. Считая, что суммы баллов, определяющие качество продукции для обеих фирм,-независимые и нормально распределенные совокупности, установить: можно ли считать, что питание, выпускаемое фирмой 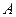, обладает значимо лучшим качеством, чем выпускаемое фирмой 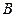? Принять уровень значимости равным =0,05.

◄ Требуется проверить основную гипотезу 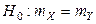против правосторонней альтернативы .

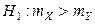Так как дисперсии точно изыестны, то имеет место случай 1. Следовательно подходящей статистикой является статистика 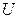, определенная в примере 5.2.2.:

.

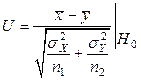
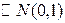Критическая область определяется условием: 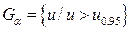, где 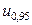=1,645 – квантиль порядка 1 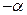=0,95 из распределения .

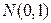Вычисляем выборочное значение статистики

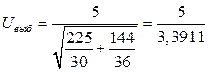=1,45.

Так как 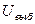<1,645, то нет оснований считать, что качество питания фирмы 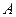значимо лучше, чем у фирмы 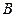(принимается основная гипотеза).►

Пример 5.3.6. Обследование, проведенное на скорость реакции среди молодых водителей по 100-балльной системе, дало следующие результаты: в группе из 21 человека, проходивших курс интенсивной подготовки на специальном автодроме, получено: 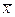=93, 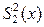=8,65. В группе же из 121 человека, проходивших обычные курсы вождения, получено: 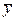=90,5; 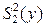=25,35.

Свидетельствуют ли эти данные о том, что интенсивный курс значимо улучшил результаты? Рассмотреть два случая: 1) =0,002 и 2) =0,05.

◄ 1) =0,002. Проверяется основная гипотеза о равенстве матожиданий против правосторонней альтернативы. Так как дисперсии неизвестны, то вначале необходимо проверить дополнительную гипотезу 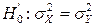против двусторонней альтернативы 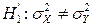. Для проверки используем фишеровскую статистику 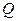, рассмотренную в примере 5.3.1

.

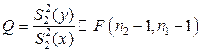Замечание. Для облегчения поиска квантилей из таблицы распределения Фишера делим большую дисперсию на меньшую. Кроме того, в этом случае, несмотря на двустороннюю альтернативу, достаточно вычислить лишь правую часть критической области, определяемую условием: 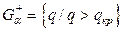, где 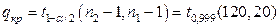=3,54. Вычисляя выборочное значение статистики, получаем: 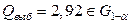, и таким образом гипотеза 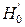принимается: дисперсии значимо не различаются.

Подходящей статистикой в этом случае является стъюдентова статистика 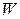из примера 5.2.3:

,

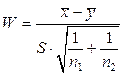
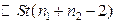где 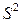- дисперсия объединенной выборки, определяемая формулой (5.3.2). В данном случае получаем 4,79. Таким образом, выборочное значение статистики получается равным 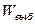=2,21. Поскольку критическая область правосторонняя, то 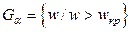, где 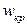находим, используя нормальную асимптотику распределения Стьюдента при большом числе степеней свободы: 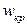= =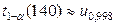2,88.

Так как 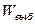< 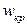, то принимается гипотеза . Следовательно интенсивные курсы не привели к значимому улучшению результатов вождения.

2) =0,05. Проверить самостоятельно, что в этом случае гипотеза 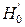о равенстве дисперсий отклоняется на данном уровне значимости. Для проверки основной гипотезы о равенстве математических ожиданий необходимо воспользоваться статистикой Уэлча (формулы (5.3.2)). Проведя вычисления по указанным формулам, находим: число степеней свободы: 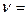44. Отсюда по таблице квантилей распределения Стьюдента 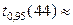1,673.

Вычисляем выборочное значение статистики 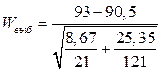=3,169.

Поскольку выборочное значение попало в критическую область, то гипотеза отвергается в пользу альтернативы: интенсивные курсы значимо улучшили скорость реакции водителей.►

Некоторые выводы. Последний пример показывает, насколько сильно могут различаться результаты проверки основной гипотезы при различных значениях . Еще раз обращаем внимание, насколько важно выбрать до всякой проверки такой уровень значимости, который бы удовлетворял всех участников эксперимента и адекватно учитывал возможные последствия от принятия решений.

Стоит также обратить внимание на такое обстоятельство. Относительная разность средних баллов, полученных для двух курсов в данном примере, составляет всего 2,7%, что часто рассматривается как величина, находящаяся в пределах так называемой статистической погрешности измерений. Тем не менее во втором случае был сделан вывод о значимости различия между результатами вождения. Немалую роль при этом играет дисперсия измерений, характеризующая их точность. В нашем примере дисперсия 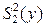почти в 3 раза выше, чем дисперсия 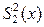. То есть измерения в малой группе проводились с существенно меньшей точностью. Этим и может быть обусловлен полученный результат.

Пример 5.3.5. Почва двух участков земли была тщательно проанализирована и оказалась одинаковой по составу. На этих участках посеяли пшеницу одного сорта. На участке 1 было внесено удобрение, а на участке 2 – нет. К моменту сбора урожая с каждого участка была произведена случайная выборка 50 растений и измерена их длина. После статистической обработки выборок были получены следующие оценки:

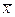=323 мм, 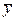=297 мм, 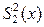=441 мм², 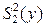=529 мм².

Можно ли на уровне значимости =0,05 считать, что внесение удобрений привело к значимому росту растений?

◄ Очевидно, речь идет о проверке основной гипотезы 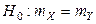против правосторонней альтернативы .

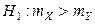Так как дисперсии неизвестны, то необходимо согласно теории проверить сначала дополнительную гипотезу 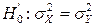против двусторонней альтернативы. Используем фишеровскую статистику 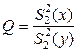из примера 5.3.1., распределенную по закону 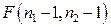. Известно (параграф 4.4), что при больших числах степеней свободы (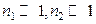) статистика Фишера асимптотически нормальна 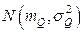, где

, ;

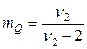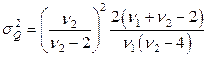отсюда следует приближенная формула для квантили порядка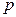

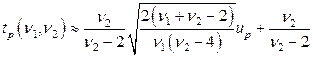, (5.3.4)

где 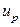- квантиль порядка 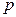из нормального распределения .

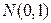Приведенная формула (5.2.4) для фишеровской квантили имеет относительную точность менее 1% уже при значениях 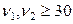. В нашем случае, учитывая двустороннюю альтернативу и используя сводку нормальных квантилей, приведенную в [1], получаем:

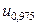=1,96; 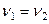=49; далее по формуле (5.2.4) 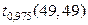=1,85 – граница части критической области на правом хвосте распределения Фишера.

По той же формуле для левой границы получаем 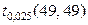=0,4395.

Вычисляем выборочное значение статистики 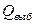=529/441=1,19.

Так как 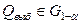, то гипотеза о равенстве дисперсий принимается.

Переходим к проверке основной гипотезы о равенстве математических ожиданий. Подходящей статистикой является стьюдентова статистика из примера 5.2.3.Так как объемы выборок равны, то выражение для статистики упрощается и приобретает вид:

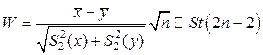
Так как число степеней свободы 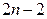=98 достаточно велико, то при вычислении критической области используем асимптотическую нормальность распределения Стьюдента: 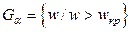, где 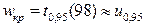=1,645.

Заметим, что вычисление указанной квантили по уточненной формуле () дает результат 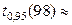1,66, что достаточно близко к полученному выше значению. Вычисляя выборочное значение статистики, получаем 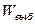=5,9. Поскольку 5,9>1,645, то гипотеза отвергается с высокой надежностью. Внесение удобрений привело к значимому увеличению урожайности.►