Общие положения, постановка задачи

Пусть закон распределения генеральной случайной величины неизвестен, но имеются те или иные основания предполагать, что генеральная распределена по закону, описываемому известной функцией распределения 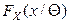, где - вектор параметров, которыми определяется данная функция (например, высказывается предположение, что .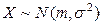

Таким образом, формулируем основную гипотезу:

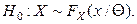
Альтернативной всегда выступает гипотеза 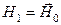, т.е. отрицающая . Критерии, используемые для проверки указанной основной гипотезы, носят название критериев согласия.

Ниже будут рассмотрены два наиболее важных для практики критерия согласия: критерий Колмогорова и критерий Пирсона (критерий хи-квадрат). Вначале обсудим некоторые общие положения, связанные с проблемой построения критериев согласия. Заметим, что как и в случае проверки уже известных нам гипотез о параметрах, для реализации критерия согласия нужна подходящая статистика, являющаяся мерой расхождения в данном случае между гипотетической функцией, утверждаемой в и эмпирической функцией распределения 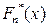(индекс 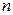подчеркивает ее зависимость от объема выборки). Всякая подходящая статистика 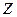должна очевидно быть функцией как от 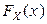, так и от 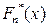, т.е. 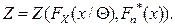. Но т.к. истинная функция распределения неизвестна, то гипотеза оказывается сложной, даже если вектор параметров 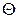- известен. В этом состоит одна из трудностей построения критериев согласия. Основное требование, предъявляемое к подходящей статистике, заключается в том, чтобы ее закон распределения при условии по крайней мере асимптотически (при 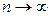) не зависел от гипотетической функции распределения.