Статистическая физика изучает системы большого числа частиц, каждая из которых описывается своим уравнением движения (уравнениями Гамильтона):
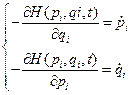
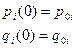 (1)
(1)
Однако из-за того, что 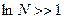 этих уравнений будет порядка 1023 и решить их все – довольно громоздкая задача. Кроме того, информация, даваемая решениями
этих уравнений будет порядка 1023 и решить их все – довольно громоздкая задача. Кроме того, информация, даваемая решениями
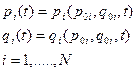 (2)
(2)
оказывается избыточной, так как нужно знать лишь небольшое число термодинамических параметров, характеризующих систему в целом (например, температуру, энтропию, энергию, давление). Поэтому для решения данной задачи нужен иной подход.
В термодинамике принято говорить о так называемых термодинамических средних значениях макроскопических параметрах по времени, так как изначально система может не находится в термодинамическом равновесии, т. е. в таком состоянии, когда значения макроскопических параметров с большой точностью равны соответствующим средним. Функция распределения по энергии для такого состояния 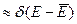 .
.
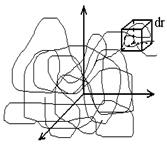 Чтобы построить термодинамическое среднее, необходимо наблюдать за системой бесконечное время. Система будет двигаться в фазовом пространстве
Чтобы построить термодинамическое среднее, необходимо наблюдать за системой бесконечное время. Система будет двигаться в фазовом пространстве 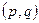 согласно уравнениям (1), описывая некоторую фазовую траекторию (2), забивающую все фазовое пространство. Если через одинаковые промежутки времени откладывать на этой траектории точки, то они заполнят все фазовое пространство с некоторой плотностью зависящей от
согласно уравнениям (1), описывая некоторую фазовую траекторию (2), забивающую все фазовое пространство. Если через одинаковые промежутки времени откладывать на этой траектории точки, то они заполнят все фазовое пространство с некоторой плотностью зависящей от 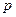 и
и 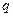 . Если
. Если 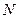 - полное число точек (
- полное число точек (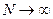 ), то число точек в данном фазовом объеме пропорционально величине этого объема
), то число точек в данном фазовом объеме пропорционально величине этого объема 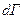
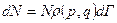
но 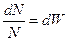 - элементарная вероятность обнаружить систему в заданном объеме за все время наблюдения.
- элементарная вероятность обнаружить систему в заданном объеме за все время наблюдения.
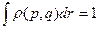 (условие нормировки).
(условие нормировки).
Среднее значение величины 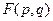
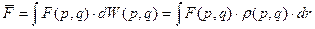 .
.
С другой стороны очевидно, что:
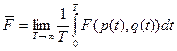 .
.
Эквивалентность двух средних и устанавливает эргодическая гипотеза.
Цель: Установить вид равновесной функции распределения 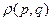 .
.
Если известно 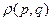 , то можно найти все средние значения микроскопических параметров
, то можно найти все средние значения микроскопических параметров 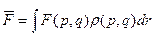
Введем также понятие функции распределения по величине F.
Построим гиперповерхности
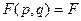
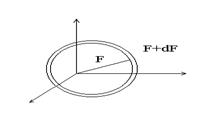
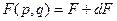
Тогда 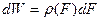 ,
, 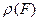 - функция распределения по
- функция распределения по 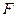 .
.
Ниже будет установлена связь между 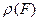 и
и 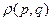 .
.
 2015-10-13
2015-10-13 709
709








