Фазовое пространство. Теорема Лиувилля

Теорема Лиувилля говорит о сохранении фазового объема, занимаемого фазовыми точками в начальный момент времени. Эти точки движутся так, что их плотность не изменяется, так, что 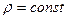. Это дает возможность установить связь между энергией и

Задачи

9. Определить фазовую траекторию тела массой 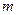, которое движется в постоянном гравитационном поле с начальной скоростью 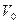(направленной вверх). Начальная координата .

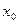Решение: Поле постоянно, следовательно, существует интеграл энергии:

.

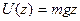
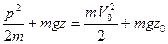Следовательно, уравнение траектории .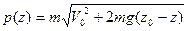

10. Определить фазовую траекторию для частиц массой 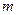и зарядом 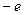, движущейся под действием силы притяжения к неподвижному заряду .

.

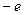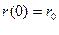
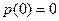Решение: Поле тяжести постоянно, так что энергия при движении сохраняется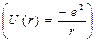

.

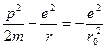Следовательно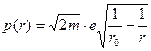

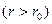
11. Определить фазовую траекторию линейного гармонического осциллятора со слабым затуханием. Как изменяется со временем фазовый объем?

Решение: Уравнение движения такого осциллятора

,

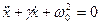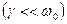
Решение этого уравнения имеет вид 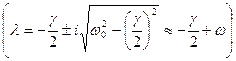- корни характеристического уравнения.

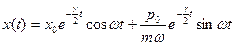
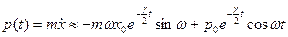
(такое решение сразу удовлетворяет начальным условиям).

Очевидно, что

,

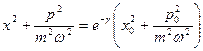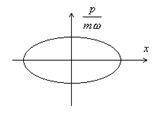то есть фазовая траектория – эллипс (в координатах 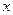и 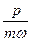- окружность радиуса 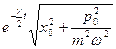). С течением времени фазовый объем 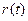(площадь круга) будет экспоненциально убывать, так, что

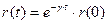
так как затухание слабое, то за период 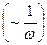радиус можно считать постоянным.

12. Определить фазовую траекторию для физического маятника массы 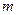. Момент инерции 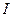, приведенная длинна .

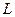Решение: Будем использовать закон сохранения энергии (как для обычных колебаний)

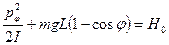
где 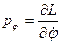- обобщенный импульс 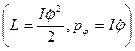. Следовательно

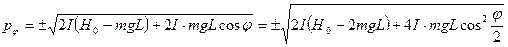
а)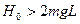

. В этом случае маятник будет совершать вращательное движение:

б) 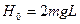. В этом случае

.

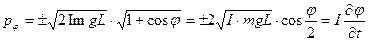Следовательно, время достижения верхней точки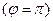

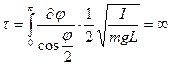
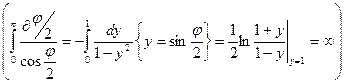
в) 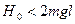. Подкоренное выражение должно быть положительным .

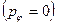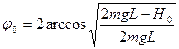- максимальный угол ().

.

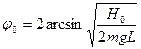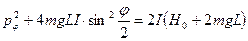В этом случае движение будет периодическим.

13. Проверить выполнимость теоремы Лиувилля для:

а) упругого столкновения двух шаров;

б) движения частиц в постоянном поле тяжести с начальными условиями , , .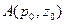

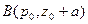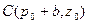Решение: а) Используем закон сохранения энергии и импульса.

.

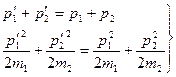
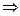
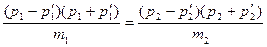Следовательно .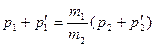

Таким образом ;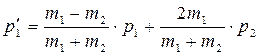

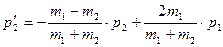
И 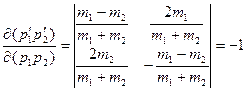, то есть фазовой объем сохраняется.

б) Уравнения движения , ,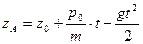

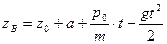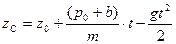
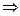
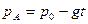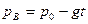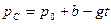
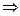
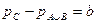, , . И следовательно 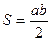в каждый момент времени.