Краткие сведения из теории вероятностей

1)Функция распределения:

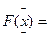Prob( 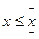) - вероятность обнаружить значение величины 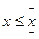. Если 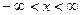, то

,

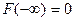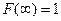
и 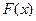- монотонно возрастающая функция. Вероятность обнаружить значение между 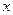и :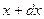

.

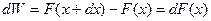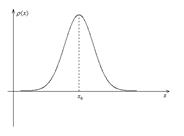
2) Плотность распределения:

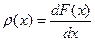- вероятность попадания 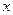в данный интервал .

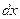Очевидно, что:

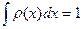(условие нормировки)

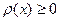
Наиболее часто встречается распределение - гауссовское:

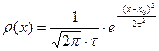
По-другому – вероятность 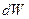пропорциональна 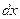или 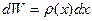. Аналогично вводится понятие плотности для нескольких случайных переменных:

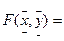Prob()

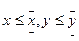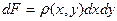или .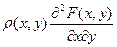

Есл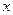и и 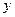независимые переменные, то вероятность обнаружить 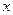не влияет на вероятность 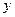, поэтому:

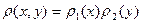
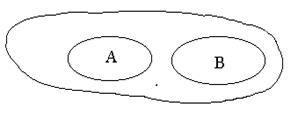NB Сложение и умножение вероятностей удобно пояснить при помощи множеств. Пусть есть множество равновероятных событий. Выделим из него два подмножества А и В. Если площадь всей фигуры на рисунке равна единице, то 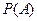порядка площади, поэтому:

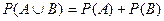( - есл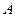и и 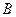не пересекаются)

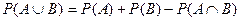( - есл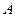и и 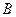пересекаются).

Условная вероятность 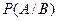- вероятность А при условии, что В произошло очевидно:

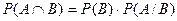
Если А и В независимы, то 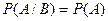и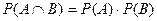

3) Среднее.

Пусть есть случайная величина А принимающая значения А_i. Тогда:

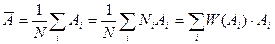
В случае непрерывной переменной .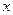

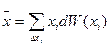
или

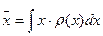- среднее (математическое ожидание или первый момент)

4) Среднеквадратичная функция, дисперсия.