Статистическим весом называется число микросостояний, реализующих заданное макросостояние.
Ex Игральные кости. Конфигурация (3 4 5), так что сумма 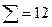 - аналог полной энергии макросостояния с
- аналог полной энергии макросостояния с 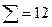 . Энтропия
. Энтропия 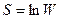 .
.
В фазовом пространстве микросостоянию соответствует ячейка объема 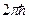 . Возьмем две гиперповерхности с энергиями
. Возьмем две гиперповерхности с энергиями 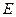 и
и 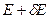 (для каждого
(для каждого 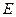
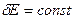 ). Число микросостояний будет пропорционально объему, заключенному между этими поверхностями
). Число микросостояний будет пропорционально объему, заключенному между этими поверхностями 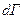 .
.
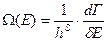 - статистический вес (число состояний на единичный интервал энергии
- статистический вес (число состояний на единичный интервал энергии 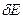 ).
).
Рассмотрим систему с постоянной энергией (замкнутая система). Плотность 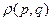 будет отлична от нуля только на гиперповерхности
будет отлична от нуля только на гиперповерхности 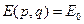 и равно нулю в остальных точках (фазовая траектория целиком лежит на этой поверхности). Кроме того
и равно нулю в остальных точках (фазовая траектория целиком лежит на этой поверхности). Кроме того 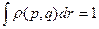 и
и 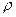 на поверхности постоянно. Этому свойству удовлетворяет
на поверхности постоянно. Этому свойству удовлетворяет 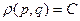
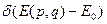 . Такое распределение называется микроканоническим.
. Такое распределение называется микроканоническим.
Найдем нормировочную константу 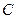 .
.
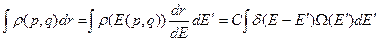 .
.
Таким образом 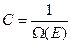 , и
, и 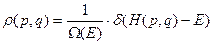 .
.
Модуль канонического распределения, температура и теплоемкость определяются как:
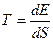 ,
, 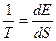 ,
, 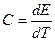 .
.
Задачи:
14. Определить 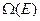 МКР для а)
МКР для а) 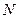 частиц идеального газа; б)
частиц идеального газа; б) 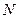 независимых линейных классических осцилляторов.
независимых линейных классических осцилляторов.
Решение: а) энергия сохраняется, следовательно
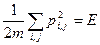
(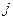 - номер проекции,
- номер проекции, 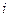 - номер частицы). Найдем объем
- номер частицы). Найдем объем 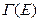 , соответствующей состояниям с энергией, меньшей
, соответствующей состояниям с энергией, меньшей 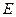 . Это, как следует из (1) будет объем
. Это, как следует из (1) будет объем 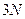 - мерного шара.
- мерного шара.
NB Объем 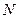 -мерного шара
-мерного шара 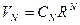 . Найдем
. Найдем 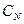 . Рассмотрим интеграл
. Рассмотрим интеграл
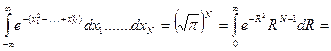
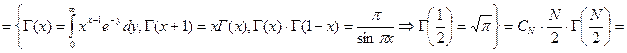
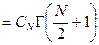 . Следовательно
. Следовательно 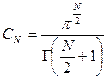 .
.
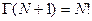
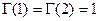 ,
, 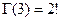
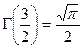 ,
, 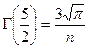
В нашем случае в роли 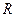 выступает
выступает 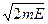 , а
, а 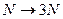 , следовательно:
, следовательно:
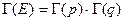
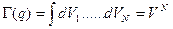
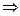
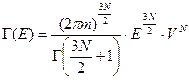
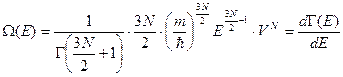
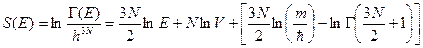 .
.
Используя уравнения термодинамики:
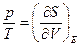
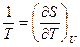
сразу получим
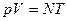 ,
, 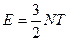
NB 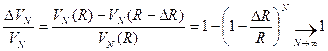
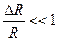 .
.
Таким образом, для больших 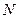 весь объем
весь объем 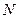 - мерной сферы заключен вблизи ее поверхности, то есть для расчета энтропии можно брать весь фазовый объем, а не только его часть вблизи поверхности.
- мерной сферы заключен вблизи ее поверхности, то есть для расчета энтропии можно брать весь фазовый объем, а не только его часть вблизи поверхности.
б) энергия системы 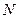 независимых трехмерных осцилляторов сохраняется и равна:
независимых трехмерных осцилляторов сохраняется и равна:
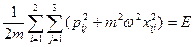

Положим 
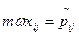 . Тогда
. Тогда
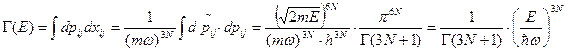 . Статистический вес:
. Статистический вес: 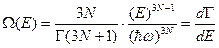 .
.
Энтропия: 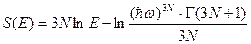
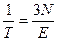 , следовательно
, следовательно 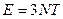 .
.
NB Заметим, что в силу того, что 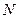 - велико
- велико
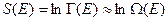 .
.
15. Вывести каноническое распределение Гиббса, взяв в качестве модели термостата примеры из предыдущей задачи.
Решение: Обозначим 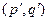 - совокупность координат и импульсов частиц термостата, а
- совокупность координат и импульсов частиц термостата, а 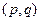 - рассматриваемой системы. Вместе они образуют замкнутую систему. Чтобы получить распределение для системы, нужно проинтегрировать
- рассматриваемой системы. Вместе они образуют замкнутую систему. Чтобы получить распределение для системы, нужно проинтегрировать 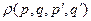 по координатам и импульсам термостата:
по координатам и импульсам термостата:
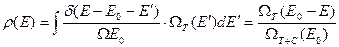 (
(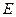 - энергия системы).
- энергия системы).
Подставим 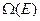 из предыдущей задачи (термостат+система содержат
из предыдущей задачи (термостат+система содержат 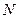 частиц, а сам термостат
частиц, а сам термостат 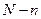 )
)
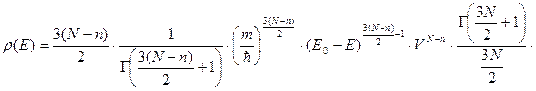
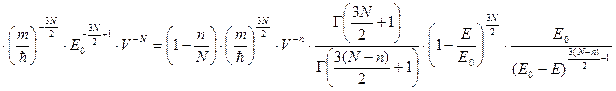 при
при
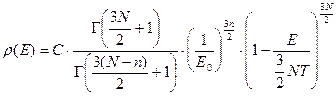
Предел 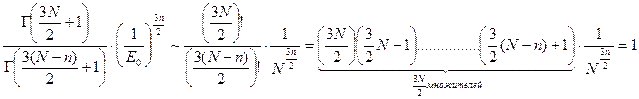
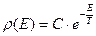 - каноническое распределение Гиббса или
- каноническое распределение Гиббса или 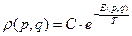 .
.
(В случае с осцилляторами следовало положить 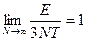 ).
).
 2015-10-13
2015-10-13 2059
2059
