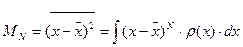
Второй центральный момент (М2) называется дисперсией 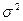
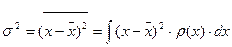
 |
Для гауссовского распределения
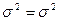
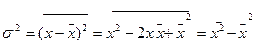
Само 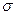 называется среднеквадратичной флуктуацией. Смысл для гауссовского распределения
называется среднеквадратичной флуктуацией. Смысл для гауссовского распределения 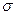 - ширина кривой по
- ширина кривой по 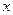 , характеризующая степень разброса
, характеризующая степень разброса 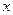 вблизи среднего. Говорить о
вблизи среднего. Говорить о 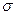 имеет смысл когда
имеет смысл когда 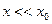
Def: 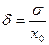 - относительная флуктуация.
- относительная флуктуация.
Задачи по теории вероятностей.
1. В корзине 20 шаров 10 черных и 10 белых. Найти вероятность того, что из трех наугад вытащенных шаров два окажутся одного цвета.
Решение: Запишем это событие в виде 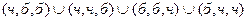 Все элементарные события – независимы, поэтому можно применять теорему о сложении вероятностей:
Все элементарные события – независимы, поэтому можно применять теорему о сложении вероятностей:
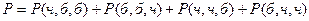
Для вычисления 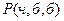 применить теорему умножения вероятностей.
применить теорему умножения вероятностей.
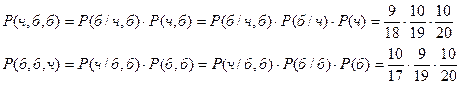
Аналогично для 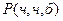 и
и 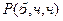 .
.
Таким образом
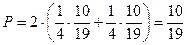
2. Три стрелка стреляют в мишень вероятность попадания одного стрелка – 0,8, второго – 0,7, третьего – 0,6. Определить вероятность того, что в мишень попало два стрелка.
Решение: Запишем это событие в виде 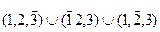
Все эти события независимы, так что вероятности просто нужно сложить (черта означает вероятность непопадания).
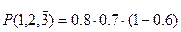 и.т.д.
и.т.д.
Так что:
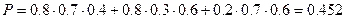
3. Определить вероятность выигрыша в 6 из 45
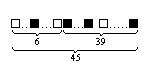
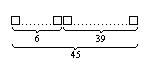 Решение:Пусть все шары вытаскивают до последнего. В результате получаем конфигурацию чисел
Решение:Пусть все шары вытаскивают до последнего. В результате получаем конфигурацию чисел 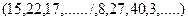 . Это можно реализовать
. Это можно реализовать 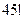 способами, причем внутри каждой группы числа могут идти в любой последовательности, например:
способами, причем внутри каждой группы числа могут идти в любой последовательности, например:
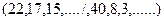 - эквивалентная конфигурация, поэтому число различных перестановок между двумя группами будет в
- эквивалентная конфигурация, поэтому число различных перестановок между двумя группами будет в 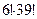 раз меньше и равно
раз меньше и равно 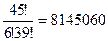
Выигрышной будет только одна комбинация, когда 6 заданных чисел выпадут первыми в любой последовательности.
5 номеров: истинных номеров среди первых шести должно быть пять (с любыми перестановками пяти истинных и одного ложного номера). При этом один истинный номер должен попасть в группу к ложным.
 Таких вариантов будет очевидно
Таких вариантов будет очевидно 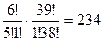
Аналогично для 4: 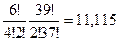
3: 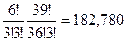
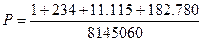
4. Плотность распределения 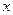
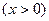
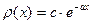
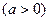 . Найти вероятность обнаружить значение
. Найти вероятность обнаружить значение 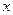 больше ее удвоенного среднего.
больше ее удвоенного среднего.
Решение:
Найдем с: 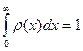
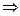
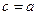
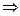
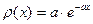
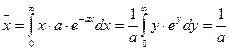
Искомая вероятность:
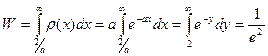
5. Плотность распределения 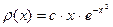
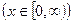 . Найти вероятность того, что при случайном наблюдении
. Найти вероятность того, что при случайном наблюдении 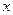 ее значение будет больше среднего.
ее значение будет больше среднего.
Решение: 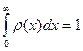
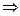
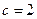
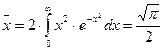 . (дифференцирование по параметру).
. (дифференцирование по параметру).
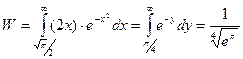
6. Случайная фаза распределена по отрезку 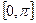 с плотностью
с плотностью 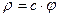 . Найти
. Найти 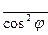 . (
. (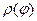 вне отрезка равна нулю).
вне отрезка равна нулю).
Решение: 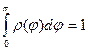 , следовательно
, следовательно 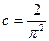 и
и 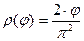
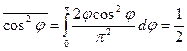

 .
.
7. Плотность распределения 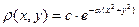 . Найти с и вероятность того, что
. Найти с и вероятность того, что 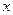 лежит в интервале
лежит в интервале 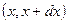
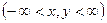 .
.
Решение: из условия нормировки находим:
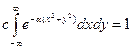
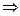
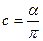 .
.
Искомая вероятность равна:
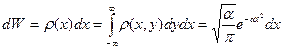 .
.
8. Математический маятник совершает колебания по закону 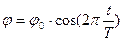 . Найти вероятность того, что при случайном измерении угла его значение будет лежать в интервале
. Найти вероятность того, что при случайном измерении угла его значение будет лежать в интервале 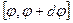 .
.
Решение: Мерой вероятности является время которое маятник проводит в данном интервале углов.
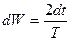 (за период данный сектор маятник проходит дважды)
(за период данный сектор маятник проходит дважды)
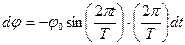
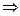
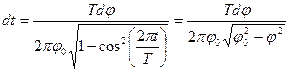
и, следовательно
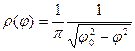 .
.
 2015-10-13
2015-10-13 1149
1149








