Это распределение получается из канонического, если воспользоваться выражением для гамильтониана 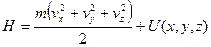 :
:
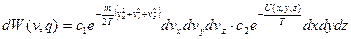 .
.
Если проинтегрировать по 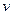 (по
(по 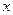 ), то эти распределения можно получить по - отдельности. Кроме того, это есть вероятность одной частице иметь координаты и скорости в заданном фазовом объеме
), то эти распределения можно получить по - отдельности. Кроме того, это есть вероятность одной частице иметь координаты и скорости в заданном фазовом объеме 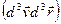 (по координатам и импульсам остальных
(по координатам и импульсам остальных 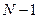 частицам
частицам 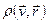 мы проинтегрировали).
мы проинтегрировали).
Задачи.
34. Получить распределение по модулю скорости, проекции и энергии для газа, не находящегося во внешнем поле.
Решение: Энергия газа 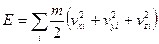 не зависит от координат. Тогда интегрирование
не зависит от координат. Тогда интегрирование 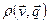 по координатам дает
по координатам дает 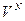 , который можно включить в нормировочный множитель (пока еще не определенный). Проинтегрировав
, который можно включить в нормировочный множитель (пока еще не определенный). Проинтегрировав 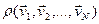 по всем скоростям, кроме одной и включив эти интегралы в
по всем скоростям, кроме одной и включив эти интегралы в 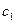 , мы получим функцию
, мы получим функцию 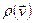 , описывающую распределение вероятностей скоростей для одной частицы:
, описывающую распределение вероятностей скоростей для одной частицы:
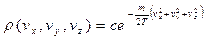 .
.
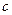 найдем из условия нормировки:
найдем из условия нормировки: 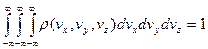 , откуда (интеграл Пуассона)
, откуда (интеграл Пуассона) 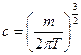 . Чтобы получить распределение по одной компоненте скорости (скажем,
. Чтобы получить распределение по одной компоненте скорости (скажем, 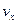 ), необходимо проинтегрировать плотность по двум остальным проекциям скорости. В результате получим:
), необходимо проинтегрировать плотность по двум остальным проекциям скорости. В результате получим:
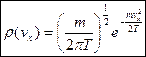 .
.
Чтобы получить распределение по модулю скорости, запишем 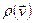 в виде:
в виде:
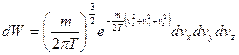 ,
,
и перейдем к сферическим координатам в пространстве скоростей:
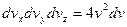 ,
, 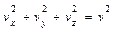 . Тогда:
. Тогда:
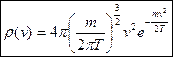
(оно автоматически оказывается нормированным).
Наконец, чтобы получить распределение по энергии, подставим 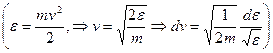 . В результате получим:
. В результате получим:
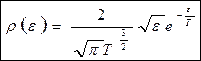
Используя эти распределения, по общим формулам, получим средние:
а) 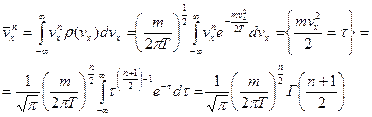
(для четных 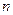 ).
).
(напомним, что 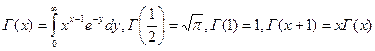 ).
).
В частности:
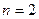 :
: 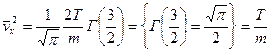 .
.
Заметим, что 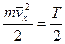 (теорема о равномерном распределении энергии по степеням свободы).
(теорема о равномерном распределении энергии по степеням свободы).
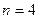
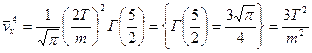 .
.
Для нечетных 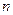
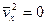 (нечетная функция).
(нечетная функция).
б) 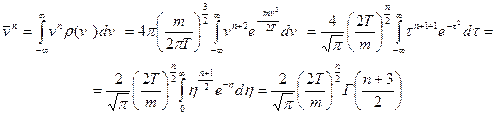 .
.
В частности:
Для 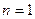
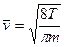 , (
, (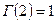 ),
),
а для 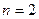
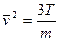 ,
, 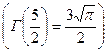 .
.
Наиболее вероятная по модулю скорость, получается дифференцированием
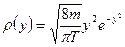 ,
, 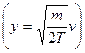 по
по 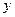 :
:
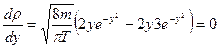 . Следовательно, при
. Следовательно, при 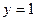
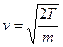
в) 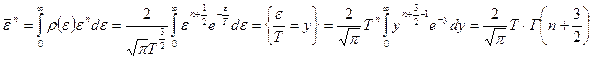 .
.
В частности при 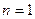
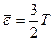 а при
а при 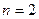
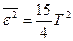 .
.
 2015-10-13
2015-10-13 572
572








