16. (Термоэлектронная эмиссия). Вероятность вылета электрона за время 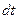 -
- 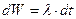 . Определить вероятность вылета
. Определить вероятность вылета 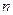 электронов за время
электронов за время 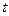 , если вылеты электронов - независимые события и промежуток времени
, если вылеты электронов - независимые события и промежуток времени 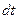 бесконечно мал (так что два электрона за это время вылететь не может). Найти также
бесконечно мал (так что два электрона за это время вылететь не может). Найти также 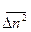 , если за время
, если за время 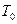 вылетит
вылетит 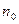 электронов.
электронов.
Решение: Разобьем интервал времени 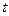 на малые участки
на малые участки 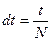 . Событие (вылет
. Событие (вылет 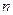 электронов за время
электронов за время 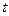 ) запишем в виде (в в н в н н…в). в – n штук, н – (N-n). Вероятность вылета -
) запишем в виде (в в н в н н…в). в – n штук, н – (N-n). Вероятность вылета - 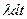 , невылета -
, невылета - 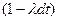 . Так как все события независимы, то по теореме умножения вероятностей:
. Так как все события независимы, то по теореме умножения вероятностей:
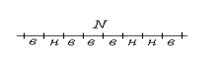
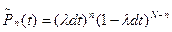
Кроме того, учтем различные перестановки между в и н. Всего их будет 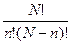 , что увеличит искомую вероятность в соответствующее число раз (так как вероятность событий (в в н в н н…в) и (в н н в н в…н) с одинаковым числом в и н одинаковы и равны
, что увеличит искомую вероятность в соответствующее число раз (так как вероятность событий (в в н в н н…в) и (в н н в н в…н) с одинаковым числом в и н одинаковы и равны 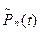 ).
).
Таким образом:
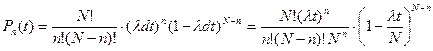
Устремим 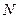 к бесконечности и учтем, что
к бесконечности и учтем, что

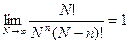 ,
, 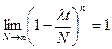 ,
, 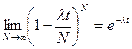


Тогда получим
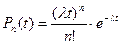
Условие нормировки 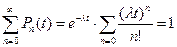 выполняется автоматически.
выполняется автоматически.
NB вероятность невылета ни одного электрона за время 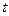
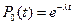 . При конечном
. При конечном 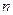 и
и 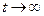 получаем
получаем 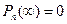 :
:
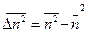
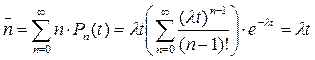
следовательно 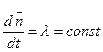 .
.
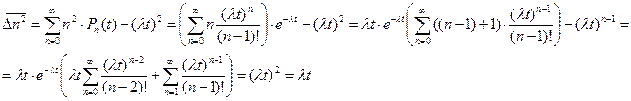
17. Идеальный газ состоящий из 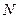 молекул, находится в объеме
молекул, находится в объеме 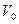 . Найти вероятность того, что в объеме
. Найти вероятность того, что в объеме 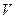
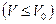 находится
находится 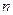 молекул.
молекул.
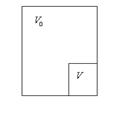
Решение: Для одной молекулы 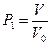 . Потребуем, чтобы
. Потребуем, чтобы 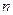 определенных молекул находились в
определенных молекул находились в 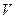
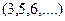 (всего
(всего 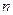 штук). При этом остальные молекулы не должны там находится. Вероятность отсутствия молекулы в объеме
штук). При этом остальные молекулы не должны там находится. Вероятность отсутствия молекулы в объеме 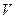
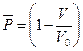 . Таким образом, вероятность того, что
. Таким образом, вероятность того, что 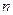 определенных молекул находятся в объеме
определенных молекул находятся в объеме 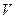 , а остальные отсутствуют ввиду некорреллированости их движений равны
, а остальные отсутствуют ввиду некорреллированости их движений равны
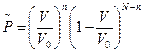 (вероятность конфигурации
(вероятность конфигурации  ,
,
(без черты - 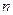 , с чертой -
, с чертой - 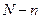 ). Таким образом,
). Таким образом,
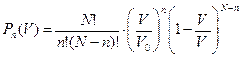 .
.
Проверим условие нормировки
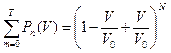
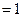 (бином Ньютона)
(бином Ньютона)
Среднее число молекул в объеме 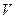 :
:
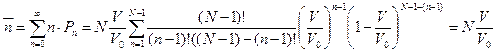
Подставим в (1)
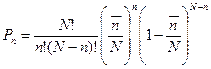
Если 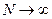 , то (см. предыдущую задачу)
, то (см. предыдущую задачу) 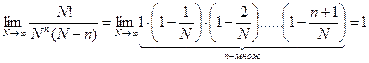
Если 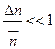 , то
, то
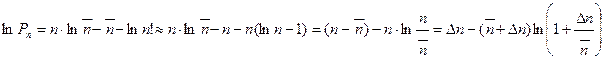
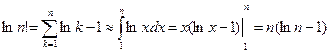 .
.
Обозначим 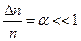 . Тогда
. Тогда
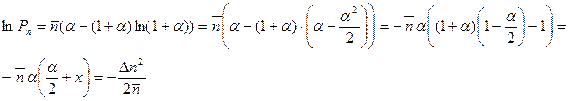
Таким образом
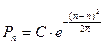
Константу 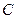 найдем из условия нормировки:
найдем из условия нормировки:
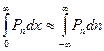
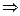
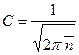
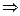
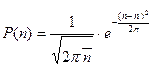 .
.
Сравнивая с гауссовским распределением, находим, что
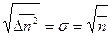
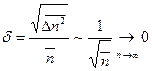
18. (Задача о случайных блужданиях по одномерной решетке). Вероятность скачка точки вправо - 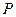 , влево -
, влево - 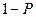 . Определить вероятность того, что за
. Определить вероятность того, что за 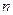 шагов частица окажется в точке с координатой
шагов частица окажется в точке с координатой 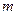 .
.
Решение: Пусть частица делает 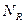 шагов вправо и
шагов вправо и 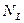 влево. Очевидно, что
влево. Очевидно, что
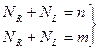
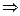
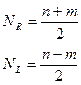 (1)
(1)
событие  - (
- ( букв «вправо» и
букв «вправо» и 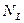 и букв «влево»).
и букв «влево»).
Вероятность такого события 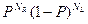 .
.
Всего таких конфигураций 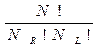 , причем все они равновероятны. По теореме о сложении вероятностей искомая вероятность равна:
, причем все они равновероятны. По теореме о сложении вероятностей искомая вероятность равна:
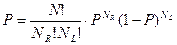
где 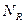 и
и 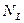 заданы в (1). Очевидно, что
заданы в (1). Очевидно, что 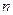 и
и 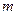 должны быть одновременно четными, либо нечетными (в противном случае вероятность равна нулю).
должны быть одновременно четными, либо нечетными (в противном случае вероятность равна нулю).
К решению данной задачи можно подойти несколько иначе. Пусть 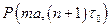 - вероятность того, что в момент времени
- вероятность того, что в момент времени 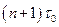 (
(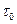 - время одного скачка) точка будет иметь координату
- время одного скачка) точка будет иметь координату 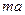 (
(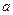 - длина одного шага). Такое событие можно реализовать двумя способами – либо в случае, когда в момент времени
- длина одного шага). Такое событие можно реализовать двумя способами – либо в случае, когда в момент времени 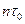 точка имела координату
точка имела координату 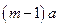 и с вероятностью
и с вероятностью 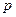 прыгнула вправо, либо когда в этот же момент ее координата была
прыгнула вправо, либо когда в этот же момент ее координата была 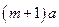 и затем с вероятностью
и затем с вероятностью 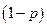 прыгнула влево. По теореме о сложении вероятностей:
прыгнула влево. По теореме о сложении вероятностей:
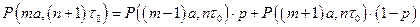 .
.
Считая 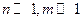 , разложим эти вероятности в ряд Тейлора:
, разложим эти вероятности в ряд Тейлора:
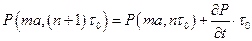 ,
,
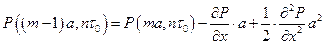 ,
,
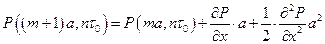 .
.
Подставляя эти выражения в исходное уравнение, получаем:
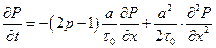 .
.
Вводя обозначения
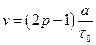 ,
, 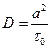 ,
,
получаем т. н. уравнение Фоккера-Планка:
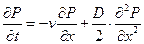 .
.
Первое слагаемое в этом уравнении описывает регулярное смещение (очевидно, при 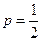 это слагаемое отсутствует, т. е. ансамбль таких точек как целое покоится), второе – т. н. диффузионное движение. Нетрудно получить решение этого уравнения при начальном условии
это слагаемое отсутствует, т. е. ансамбль таких точек как целое покоится), второе – т. н. диффузионное движение. Нетрудно получить решение этого уравнения при начальном условии
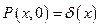
Применяя преобразование Фурье по координате к вероятности:
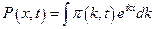
Получаем для Фурье – образа 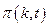 :
:
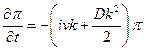 ,
,
Откуда после интегрирования находим:
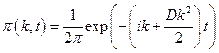 (с учетом начального условия
(с учетом начального условия 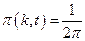 )
)
Подставляя в последний интеграл и вычисляя его, получаем нормированное распределение:
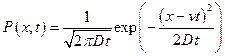 ,
,
характерная ширина которого изменяется со временем по закону 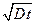 , что характерно для диффузионного движения (вспомните броуновскую частицу). Максимум же смещается равномерно со скоростью
, что характерно для диффузионного движения (вспомните броуновскую частицу). Максимум же смещается равномерно со скоростью 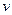 , что соответствует регулярному сносу. Если
, что соответствует регулярному сносу. Если 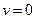 , то получается чисто диффузионное движение (такой процесс называется винеровским), если же
, то получается чисто диффузионное движение (такой процесс называется винеровским), если же 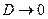 , то используя одно из предельных представлений
, то используя одно из предельных представлений 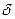 - функции, получаем детерминированное движение:
- функции, получаем детерминированное движение:
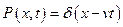 .
.
19. Определить энергию, температуру, энтропию, статистический вес и теплоемкость состояния с полной энергией 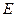 системы независимых квантовых осцилляторов, считая, что частоты всех осцилляторов одинаковы.
системы независимых квантовых осцилляторов, считая, что частоты всех осцилляторов одинаковы.
Решение: Энергия одного осциллятора 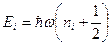 ,
, 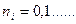
Энергия всей системы равна сумме энергий всех осцилляторов:

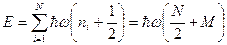 ,
, 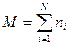
Таким образом, макросостояние задается числом 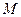 . В то же время данное
. В то же время данное 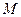 получается различными конфигурациями
получается различными конфигурациями 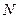 целых положительных чисел, сумма которых равна
целых положительных чисел, сумма которых равна 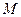 :
: 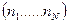 . Необходимо найти всевозможные такие конфигурации. Их число и есть статистический вес состояния с энергией
. Необходимо найти всевозможные такие конфигурации. Их число и есть статистический вес состояния с энергией 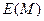 . Запишем данную конфигурацию так
. Запишем данную конфигурацию так 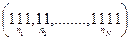 - всего
- всего 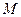 единиц и
единиц и 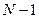 запятых. Очевидно, все конфигурации можно получить перестановками единиц и запятых. Всего их
запятых. Очевидно, все конфигурации можно получить перестановками единиц и запятых. Всего их
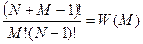
Энтропия:
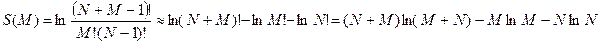
Температура:
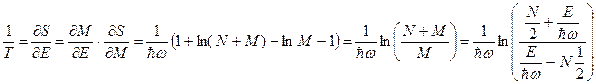
(так как 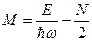
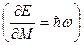 ).
).
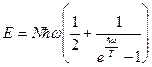
(формула Эйнштейна). Предельные случаи:
а) 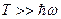
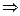
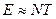
б) 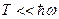
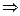
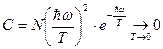

20. 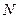 частиц могут находиться на двух энергетических уровнях
частиц могут находиться на двух энергетических уровнях 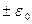 . Найти среднюю энергию, температуру, энтропию, статистический вес и теплоемкость.
. Найти среднюю энергию, температуру, энтропию, статистический вес и теплоемкость.
Решение: Пусть 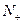 частиц имеющих энергию
частиц имеющих энергию 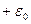 , а
, а 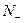 -
- 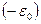 . Энергия такой конфигурации
. Энергия такой конфигурации
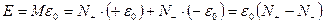
откуда
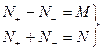 . Следовательно
. Следовательно 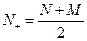
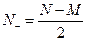 .
.
Кроме того, данное значение энергии может быть реализовано 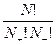 способами. Это и будет статистическим весом состояния с энергией
способами. Это и будет статистическим весом состояния с энергией 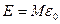 :
:
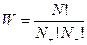
Энтропия:
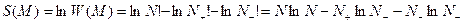 .
.
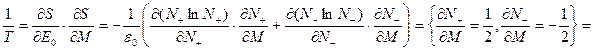
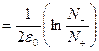 . Таким образом, получаем:
. Таким образом, получаем:
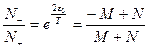
или 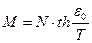 , откуда
, откуда
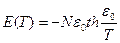 .
.
Предельные случаи
а) 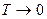
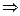
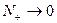
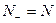
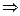
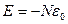 (энергия системы минимальна)
(энергия системы минимальна)
б) 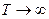
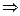
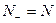
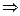
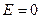 (полное разупорядочение).
(полное разупорядочение).
Теплоемкость
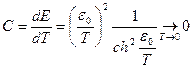 .
.
21. Один интересный метод получения распределения Гиббса.
Рассмотрим сосуд, объемом 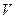 , содержащий
, содержащий 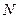 одинаковых частиц идеального одноатомного газа. Мысленно разобьем его на
одинаковых частиц идеального одноатомного газа. Мысленно разобьем его на 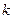 одинаковых частей, в каждой из которых в данный момент будет находиться
одинаковых частей, в каждой из которых в данный момент будет находиться 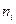 частиц (
частиц (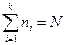 ). Такую конфигурацию назовем микросостоянием и введем для нее обозначение
). Такую конфигурацию назовем микросостоянием и введем для нее обозначение 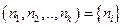
Ввиду тождественности рассматриваемых частиц указанную конфигурацию можно реализовать 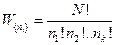 одинаковым способами, соответствующими перестановкам частиц внутри каждого объема. Такую величину назовем термодинамическим весом данного макросостояния, а ее логарифм – энтропией
одинаковым способами, соответствующими перестановкам частиц внутри каждого объема. Такую величину назовем термодинамическим весом данного макросостояния, а ее логарифм – энтропией 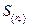 .
.
Т. к. обычно приходится иметь дело с термодинамической системой, где все 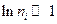 , то выражение для энтропии можно записать приближенно, воспользовавшись формулой Стирлинга
, то выражение для энтропии можно записать приближенно, воспользовавшись формулой Стирлинга 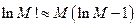 :
:
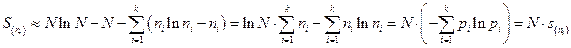
 где
где 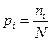 - вероятность нахождения определенных
- вероятность нахождения определенных 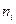 частиц в объеме
частиц в объеме 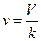 . Очевидно, что
. Очевидно, что 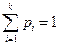 . Вместо
. Вместо 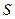 введена энтропия в расчете на одну частицу
введена энтропия в расчете на одну частицу 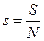 .
.
Выясним, какой конфигурации чисел 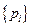 будет соответствовать максимальное значение удельной энтропии. Трудность здесь заключается в том, что
будет соответствовать максимальное значение удельной энтропии. Трудность здесь заключается в том, что 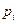 не являются независимыми переменными, а подчиняются условию нормировки
не являются независимыми переменными, а подчиняются условию нормировки 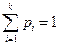 . В этом случае, согласно методу неопределенных множителей Лагранжа, будем исследовать на максимум не
. В этом случае, согласно методу неопределенных множителей Лагранжа, будем исследовать на максимум не 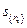 , а величину
, а величину 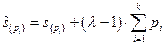 . Это позволяет учесть условие нормировки, при этом считая
. Это позволяет учесть условие нормировки, при этом считая 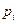 уже независимыми. Подставляя сюда
уже независимыми. Подставляя сюда 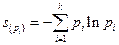 и выполняя дифференцирование, получаем условие максимума:
и выполняя дифференцирование, получаем условие максимума:
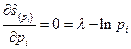 ,
,
откуда можно заключить, что максимуму энтропии соответствуют 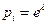 , одинаковые для каждого объема. Поэтому, как следует из условия нормировки
, одинаковые для каждого объема. Поэтому, как следует из условия нормировки 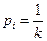 и
и 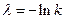 . Это означает, что в состоянии с максимальной энтропией частицы рассредоточены равномерно по всему объему сосуда.
. Это означает, что в состоянии с максимальной энтропией частицы рассредоточены равномерно по всему объему сосуда.
Если взять достаточно большое 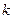 , то мы получим континуальный предел. Тогда вместо вероятностей можно писать
, то мы получим континуальный предел. Тогда вместо вероятностей можно писать 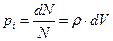 , где
, где 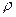 - плотность распределения частиц по объему. Для энтропии в этом случае справедливо представление:
- плотность распределения частиц по объему. Для энтропии в этом случае справедливо представление:
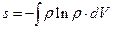 ,
,
т. е. энтропия получается как среднее от логарифма функции распределения.
Однако рассмотренная задача, как и само понятие «конфигурация», естественно, нуждаются в обобщении. Дело в том, что мы рассматривали все частицы как неподвижные, в то время как в действительности они движутся с определенными скоростями и таким образом, конфигурация частиц будет задаваться уже как 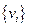 . Такое обозначение позволяет судить о количестве частиц в
. Такое обозначение позволяет судить о количестве частиц в 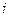 -й части в пространстве скоростей с одним лишь отличием от случая пространственного распределения – оно не имеет конечного «объема», т. к. скорость частицы может принимать любые значения. Однако и здесь есть определенные ограничения. Дело в том, что при движении полная энергия частиц должна сохраняться. Считая для простоты (обобщение очевидно), что частицы обладают только кинетической энергией и, обозначив
-й части в пространстве скоростей с одним лишь отличием от случая пространственного распределения – оно не имеет конечного «объема», т. к. скорость частицы может принимать любые значения. Однако и здесь есть определенные ограничения. Дело в том, что при движении полная энергия частиц должна сохраняться. Считая для простоты (обобщение очевидно), что частицы обладают только кинетической энергией и, обозначив 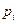 - относительное число частиц, обладающих энергией
- относительное число частиц, обладающих энергией 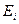 , можно теперь сформулировать задачу следующим образом. Требуется найти максимум функции
, можно теперь сформулировать задачу следующим образом. Требуется найти максимум функции 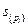 , но уже при двух дополнительных условиях – постоянства величин
, но уже при двух дополнительных условиях – постоянства величин 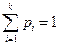 и
и 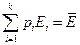 , связывающих между собой
, связывающих между собой 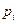 . Умножая последние два выражения на
. Умножая последние два выражения на 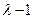 и
и 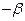 соответственно и прибавляя их к
соответственно и прибавляя их к 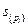 , получаем, что мы теперь должны исследовать на максимум величину
, получаем, что мы теперь должны исследовать на максимум величину
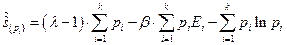
считая все 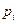 независимыми.
независимыми.
Из условия 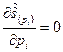 находим уравнение:
находим уравнение:
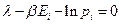 ,
,
откуда
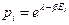
Вводя обозначение 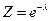 из условия нормировки, сразу находим
из условия нормировки, сразу находим 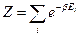 . Эту величину назовем статистической суммой, а
. Эту величину назовем статистической суммой, а 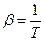 (
(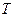 - абсолютная температура) – модулем канонического распределения. Полученное выражение представляет собой распределение частиц по энергетическим уровням и называется каноническим распределением Гиббса:
- абсолютная температура) – модулем канонического распределения. Полученное выражение представляет собой распределение частиц по энергетическим уровням и называется каноническим распределением Гиббса:
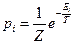 ,
, 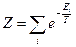 .
.
Используя 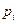 , найдем среднюю энергию системы (на одну частицу):
, найдем среднюю энергию системы (на одну частицу):
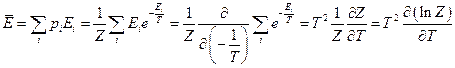
и аналогичным образом энтропию и свободную энергию 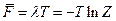 .
.
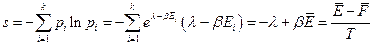 .
.
В случае, если имеются и другие аддитивные, сохраняющиеся для всей системы величины 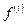 (например, число частиц
(например, число частиц 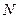 ), то, выполняя аналогичную процедуру, получим, что вероятность для системы иметь значения соответствующих величин
), то, выполняя аналогичную процедуру, получим, что вероятность для системы иметь значения соответствующих величин 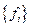 будет равна:
будет равна:
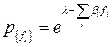 .
.
 2015-10-13
2015-10-13 1253
1253

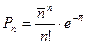 (
(