- В классическом случае плотность вероятности:
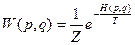 , где
, где 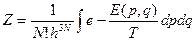
Такое распределение справедливо для системы в термостате (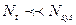 ). Величина
). Величина 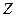 называется статистическим интегралом.
называется статистическим интегралом.
- В квантовом случае плотность вероятности:
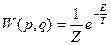 , где
, где 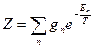 .
.
Величина 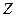 называется статистической суммой,
называется статистической суммой, 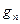 – кратность вырождения
– кратность вырождения 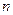 -го уровня. При помощи статистического интеграла можно определить все термодинамические характеристики системы (средние):
-го уровня. При помощи статистического интеграла можно определить все термодинамические характеристики системы (средние):
а) Свободная энергия 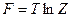 ;
;
б) Внутренняя энергия 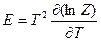 ;
;
в) Энтропия 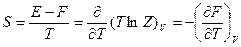 ;
;
г) Уравнение состояния 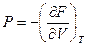 ;
;
д) Теплоемкость 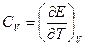 .
.
NB Наличие множителя 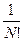 говорит, о том, что это вероятность данной конфигурации
говорит, о том, что это вероятность данной конфигурации 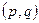 безотносительно к тому, какие частицы обладают данными
безотносительно к тому, какие частицы обладают данными 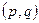 (Такая вероятность в
(Такая вероятность в 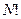 раз больше, чем вероятность одной частице иметь импульсы и координаты
раз больше, чем вероятность одной частице иметь импульсы и координаты 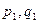 , второй -
, второй - 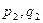 и т.д.). Кроме того, заметим, что статистический интеграл обладает свойством мультипликативности, т.е. если гамильтониан представим в виде
и т.д.). Кроме того, заметим, что статистический интеграл обладает свойством мультипликативности, т.е. если гамильтониан представим в виде 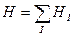 , то
, то 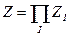 .
.
Задачи
- Для идеального газа в объеме
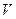 определить
определить 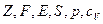 . Газ одноатомный и содержит
. Газ одноатомный и содержит 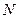 частиц.
частиц.
Решение: Гамильтониан невзаимодействующих частиц в отсутствии внешнего поля имеет вид: 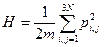 и не зависит от координат. Следовательно,
и не зависит от координат. Следовательно, 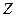 обладает свойством мультипликативности. В этом случае
обладает свойством мультипликативности. В этом случае
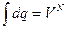 ,
,
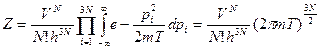 .
.
Воспользовавшись формулой Стирлинга (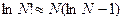 ), получаем:
), получаем:
Свободная энергия 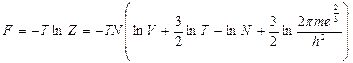 ;
;
Энтропия: 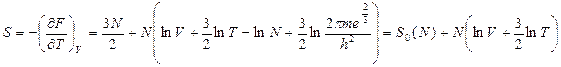 ;
;
Внутренняя энергия 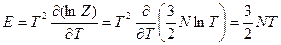 ;
;
Уравнение состояния: 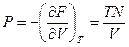 , откуда сразу получаем уравнение Менделеева - Клайперона
, откуда сразу получаем уравнение Менделеева - Клайперона 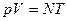 .
.
Теплоемкость 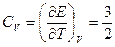 .
.
- То же для ультрарелятивистского газа
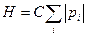 .
.
Решение: Воспользуемся сферической симметрией в импульсном пространстве и мультипликативностью 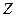 :
:
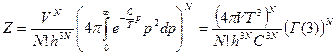 = {
= { 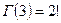 - Гамма-функция} =
- Гамма-функция} = 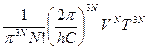 .
.
Отсюда сразу получаем:
Свободная энергия 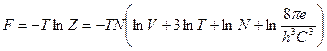 ;
;
Энтропия: 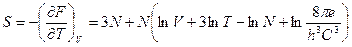 ;
;
Внутренняя энергия 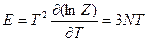 (как для осциллятора, см. ниже.);
(как для осциллятора, см. ниже.);
Уравнение состояние: 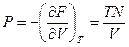 (как для идеального газа)
(как для идеального газа)
Теплоемкость 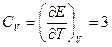 .
.
- Рассмотреть парадокс Гиббса.
Решение: П.Г. заключается в возрастании энтропии в 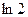 раз при соединении двух одинаковых сосудов с одинаковым числом частиц и температурой. Однако если переписать энтропию в виде (см. зад. 1 и 2):
раз при соединении двух одинаковых сосудов с одинаковым числом частиц и температурой. Однако если переписать энтропию в виде (см. зад. 1 и 2):
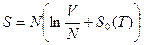 , то парадокс снимается:
, то парадокс снимается:
до соединения 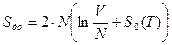
и после 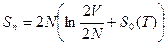 . Так что
. Так что 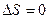 как и должно быть.
как и должно быть.
- Определить
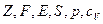 для системы из
для системы из 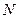 независимых классических одномерных осцилляторов.
независимых классических одномерных осцилляторов.
Решение:
Гамильтониан 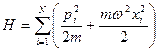 , статистический интеграл
, статистический интеграл 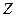 обладает мультипликативностью, если формально рассматривать
обладает мультипликативностью, если формально рассматривать 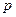 и
и 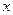 как независимые переменные:
как независимые переменные:
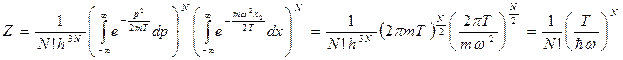 ;
;
Свободная энергия 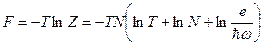 ;
;
Энтропия: 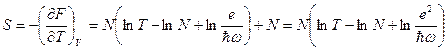 ;
;
Внутренняя энергия 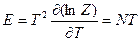 ;
;
Теплоемкость 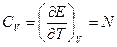 .(закон Дюлонга – Пти, в кристалле
.(закон Дюлонга – Пти, в кристалле 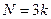 , где
, где 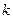 – число атомов).
– число атомов).
- То же для квантового осциллятора (рассмотреть предельные случаи).
Решение: Кратность вырождения энергетических уровней осциллятора равна единице.
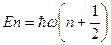 ,
, 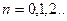
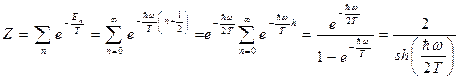 ;
;
Свободная энергия 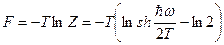 ;
;
Внутренняя энергия
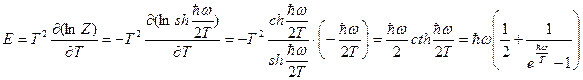 ;
;
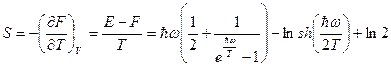
Теплоемкость 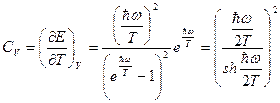 .
.
Предельный случай высоких температур 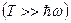
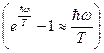
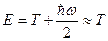 ,
, 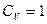
Низкие температуры 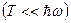
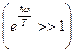 :
:
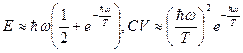 ,
, 
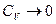 при
при 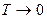 .
.
- То же для квантового ротатора.
NB Квантовый ротатор – груз массы 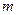 , вращающийся на нерастяжимой нити длины
, вращающийся на нерастяжимой нити длины 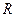 , так что его траектория лежит на сфере радиуса
, так что его траектория лежит на сфере радиуса 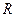 . Зависимость волновых функций от
. Зависимость волновых функций от 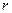 дается множителем
дается множителем 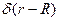 , а для угловой части
, а для угловой части 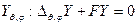
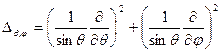 ,
, 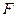 – собственные значения абсолютной величины момента.
– собственные значения абсолютной величины момента.
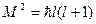 , вращательная энергия
, вращательная энергия 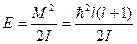 ,
, 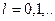
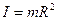 - момент инерции ротатора.
- момент инерции ротатора.
Решение: Кратность вырождения 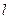 –го уровня равна
–го уровня равна 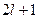 (по возможным направлениям момента), следовательно
(по возможным направлениям момента), следовательно
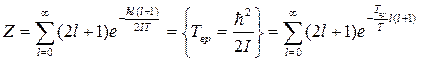 .
.
Точно данная сумма не считается. Рассмотрим предельные случаи.
1) 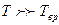 , следовательно, аргумент в экспоненте – малая отрицательная величина и
, следовательно, аргумент в экспоненте – малая отрицательная величина и 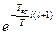 - медленно меняющаяся функция
- медленно меняющаяся функция 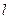 . Тогда сумму можно заменить интегралом:
. Тогда сумму можно заменить интегралом:
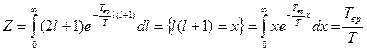 .
.
Средняя энергия 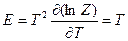 , теплоемкость
, теплоемкость 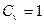 (классический предел).
(классический предел).
2) 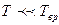 следовательно, аргумент в экспоненте – большая отрицательная величина и
следовательно, аргумент в экспоненте – большая отрицательная величина и 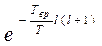 - быстро спадающая функция. Тогда в
- быстро спадающая функция. Тогда в 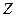 можно ограничится двумя слагаемыми (
можно ограничится двумя слагаемыми (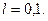 ).
).
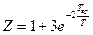 ,
, 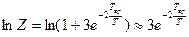 .
.
Средняя энергия 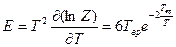 , теплоемкость
, теплоемкость 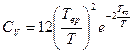 ;
;
Свободная энергия 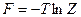 при
при 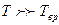
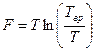
а при 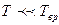
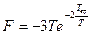 (стремится к нулю при
(стремится к нулю при 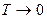 ).
).
Энтропия 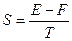 при
при 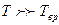
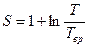 ,
,
а при 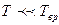
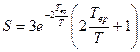 (стремится к нулю при
(стремится к нулю при 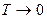 ).
).
- То же для одномерной модели Изинга ферромагнетика. Число магнитных моментов
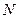 .
.
Решение: Модель Изинга является наиболее распространенной моделью взаимодействия соседних спинов, равных ½. Энергия взаимодействия 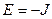 – если соседние спины параллельны и
– если соседние спины параллельны и 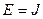 если спины антипараллельны.
если спины антипараллельны.
Число взаимодействующих пар 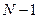 . Пусть
. Пусть 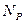 – число пар с параллельными спинами,
– число пар с параллельными спинами, 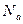 – с антипараллельными. Тогда
– с антипараллельными. Тогда 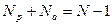 , а энергия такой конфигурации:
, а энергия такой конфигурации:
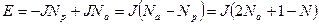 .
.
Кратность вырождения (статистический вес) такого состояния (с данным 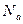 ) равен
) равен 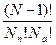 . Кроме того, число состояний с заданной энергией вдвое больше, т.к. при изменении направления всех спинов на противоположные энергия не изменяется.
. Кроме того, число состояний с заданной энергией вдвое больше, т.к. при изменении направления всех спинов на противоположные энергия не изменяется. 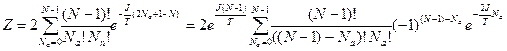 = =
= = 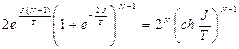 ,
,
(здесь мы воспользовались биномом Ньютона). Отсюда свободная энергия 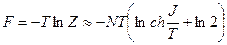 ;
;
Энтропия 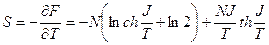 ;
;
Средняя энергия 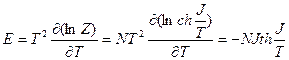 ,
,
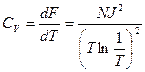 ,(стремится к нулю при
,(стремится к нулю при 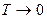 )..
)..
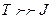
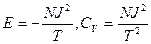
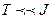
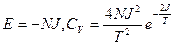 .
.
- Твердое тело состоит из
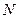 невзаимодействующих ядер со спином 1. Каждое ядро может находиться в одном из трех квантовых состояний
невзаимодействующих ядер со спином 1. Каждое ядро может находиться в одном из трех квантовых состояний 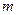 (
(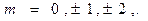 ). Вследствие электрического взаимодействия с внутренними полями в твердом теле, состояния с
). Вследствие электрического взаимодействия с внутренними полями в твердом теле, состояния с 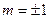 вырождены, т.е. имеют энергию
вырождены, т.е. имеют энергию 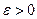 ;
; 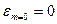 . Найти
. Найти 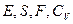 . Рассмотреть предельные случаи.
. Рассмотреть предельные случаи.
Решение: Т.к. частицы не взаимодействуют, то статистическая сумма 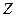 обладает свойством мультипликативности, т.е.
обладает свойством мультипликативности, т.е.
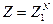 , где
, где 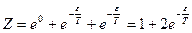 , т.к. состояния с
, т.к. состояния с 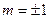 обладают одинаковой энергией
обладают одинаковой энергией 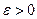 .Тогда
.Тогда 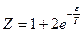 и
и 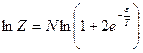 .
.
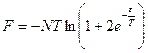 ;
;
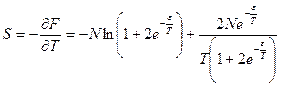 ;
;
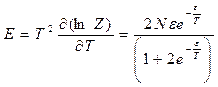 ;
;
при 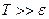
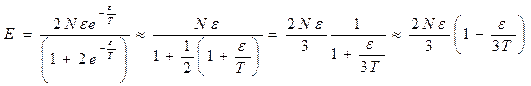
при 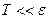
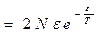
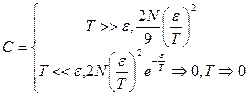
- Определить диэлектрическую (магнитную) проницаемость газа из
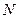 дипольных (магнитных) моментов
дипольных (магнитных) моментов 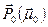 , находящихся в однородном внешнем поле
, находящихся в однородном внешнем поле 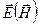 .
.
NB Определенный здесь «газ» не означает газ в обычном смысле. Предполагается, что моменты не взаимодействуют друг с другом. А так «газом» могут быть и твердые тела.
Решение: I способ. Выражение для плотности свободной энергии 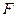 должно включать и работу по намагничиванию единицы объема магнетика и изменению энергии момента в поле
должно включать и работу по намагничиванию единицы объема магнетика и изменению энергии момента в поле 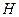 , т.е. в сумме – работу поля при его изменении на
, т.е. в сумме – работу поля при его изменении на 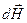 :
: 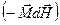 .
.
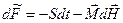
равновесная намагниченность (магнитный момент единицы объема):
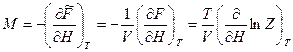 =
=
{в силу мультипликативности гамильтониана, т.к. моменты не взаимодействуют}
= 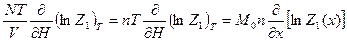 ,
,
где 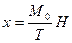 , а
, а 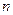 – концентрация.
– концентрация.
Гамильтониан одного момента 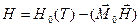 , следовательно
, следовательно
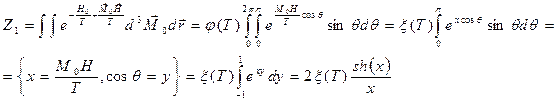
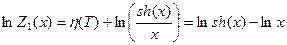 ,
,
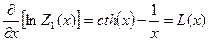 - функция Ланжевена
- функция Ланжевена
Асимптотики:
а) большие 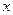 (большие поля или низкие температуры)
(большие поля или низкие температуры)
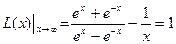
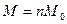 - все магнитные моменты выстраиваются по полю.
- все магнитные моменты выстраиваются по полю.
б) малые 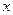 (малые поля или высокие температуры)
(малые поля или высокие температуры)
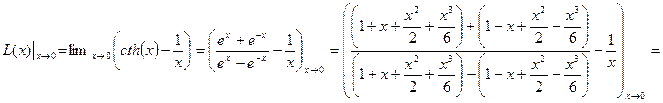
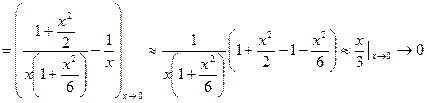
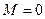 – все магнитные моменты разупорядочиваются.
– все магнитные моменты разупорядочиваются.
Поскольку реально напряженность поля много меньше микроскопической напряженности молекулярного поля, то в первом приближении:
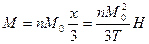 .
.
отсюда магнитная проницаемость 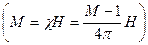 .
.
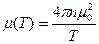 (
(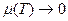 при
при 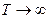 ).
).
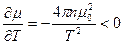 .
.
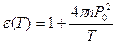 .
.
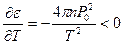 .
.
Для магнетокалорического эффекта:
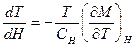 , при низких температурах
, при низких температурах 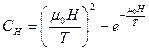 ,
, 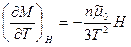 à
à
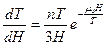 , которое может быть решено численно.
, которое может быть решено численно.
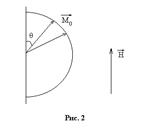 II способ. Рассмотрим сферу радиуса
II способ. Рассмотрим сферу радиуса 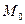 . Возможны любые ориентации
. Возможны любые ориентации 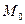 относительно
относительно 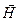 . Число магнитных моментов в бесконечно малом телесном углу
. Число магнитных моментов в бесконечно малом телесном углу 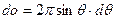 дается распределением Больцмана (см. ниже):
дается распределением Больцмана (см. ниже):
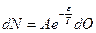 ,
,
где 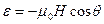 .
.
Обозначим 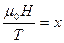 , тогда
, тогда 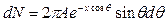 и
и
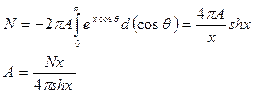
Тогда
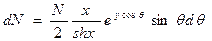 .
.
Вклад в суммарную проекцию магнитного момента единицы объема от моментов, лежащих в этом интервале углов:
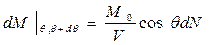
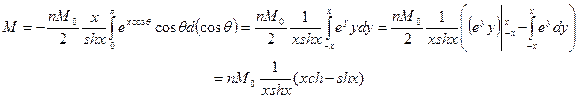
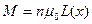 ,
,
где 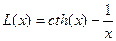 - функция Ланжевена.
- функция Ланжевена.
31. Три частицы со спином 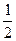 расположены по углам равностороннего треугольника. Гамильтониан спин-спинового взаимодействия трех частиц:
расположены по углам равностороннего треугольника. Гамильтониан спин-спинового взаимодействия трех частиц: 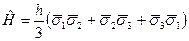 . Найти уровни энергии, их кратность вырождения, функцию распределения и термодинамические характеристики.
. Найти уровни энергии, их кратность вырождения, функцию распределения и термодинамические характеристики.
Решение: Полный спин системы 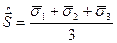 . Отсюда следует с учетом того, что
. Отсюда следует с учетом того, что 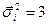 (матрицы Паули), получаем
(матрицы Паули), получаем 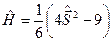 . Так как собственные значения
. Так как собственные значения 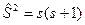 , то отсюда можно найти значения энергии, соответствующие полному спину
, то отсюда можно найти значения энергии, соответствующие полному спину 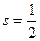 и
и 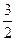 . (¯ и ).
. (¯ и ).
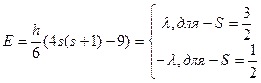
Кратность вырождения уровня с 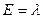 равна 4 (4 проекции полного спина
равна 4 (4 проекции полного спина 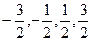 ), а уровня с
), а уровня с 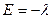 равна 2. Но так как существует два независимых способа образовать из 3–х частиц со спином ½ состояние со спином ½, то кратность также равна 4. Статистический интеграл тогда имеет вид:
равна 2. Но так как существует два независимых способа образовать из 3–х частиц со спином ½ состояние со спином ½, то кратность также равна 4. Статистический интеграл тогда имеет вид:
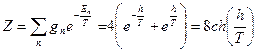
Отсюда находим термодинамические характеристики:
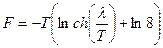
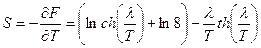
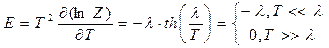
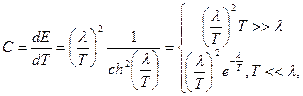
 , при
, при 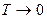
- LC – контур используется в качестве термометра. При этом измеряется возникающее в цепи нулевое напряжение на индуктивности и емкости, включенных параллельно. Вывести соотношения, связывающее среднеквадратичное значение шумового напряжения с абсолютной температурой.
Решение: Энергия колебательного контура:
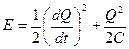
частота таких колебаний, очевидно, равна 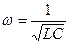 .
.
Следовательно, собственные значения энергии равны 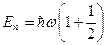 , а средняя энергия равна (ср. с задачей 5):
, а средняя энергия равна (ср. с задачей 5):
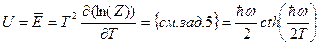 .
.
Но
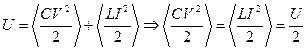 .
.
Подставляя 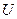 , находим:
, находим:
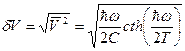 ,
, 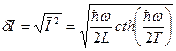 .
.
Предельные случаи:
1) 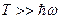 (ср. с задачей 9):
(ср. с задачей 9): 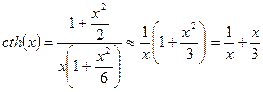
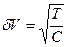 ,
, 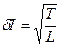
2) 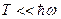 :
: 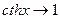 при
при 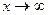 . Следовательно
. Следовательно 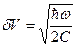 ,
, 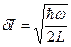 .
.
- Температурная зависимость молярной теплоемкости
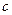 , обусловленной переходом ионов со спином ½ из парамагнитного состояния в ферромагнитное имеет вид:
, обусловленной переходом ионов со спином ½ из парамагнитного состояния в ферромагнитное имеет вид: 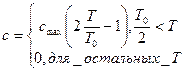 . Найти
. Найти 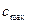 .
.
Решение: Из термодинамики следует, что 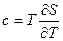 , откуда изменение энтропии при нагревании от
, откуда изменение энтропии при нагревании от 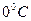 до
до 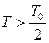 :
:
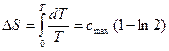
Найдем 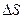 из статистики:
из статистики: 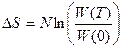 .
.
При 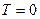 все спины параллельны,
все спины параллельны, 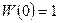 и следовательно
и следовательно 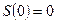 .
.
При 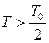 система не может поглощать тепло (
система не может поглощать тепло (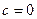 ), следовательно, она имеет максимальную энтропию. В этом состоянии все спины неколлинеарны и
), следовательно, она имеет максимальную энтропию. В этом состоянии все спины неколлинеарны и 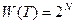 (
(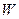 – число различных состояний системы (для
– число различных состояний системы (для 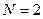 , ¯, ¯,¯¯
, ¯, ¯,¯¯ 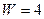 )). Таким образом
)). Таким образом 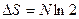 .
.
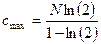 .
.
 2015-10-13
2015-10-13 3089
3089








