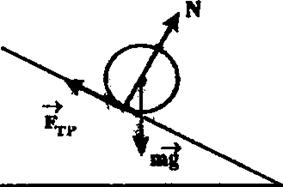
Рассмотрим качение цилиндра или шара по наклонной плоскости, образующей угол α с горизонтом (рис. 3). На цилиндр действуют три силы: сила тяжести 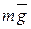 , сила нормального давления плоскости на цилиндр
, сила нормального давления плоскости на цилиндр 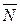 и сила трения цилиндра и плоскости
и сила трения цилиндра и плоскости 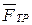 .
.
Запишем уравнение динамики поступательного движения, считая, что все силы приложены к центру масс:
 |
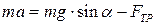 (4.1)
(4.1)
где 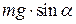 — проекция силы тяжести, направленная вдоль наклонной плоскости.
— проекция силы тяжести, направленная вдоль наклонной плоскости.
При скатывании с наклонной плоскости цилиндр вращается относительно оси, совпадающей с геометрической осью цилиндра. В уравнении динамики вращательного движения цилиндра относительно оси, проходящей через центр масс, необходимо учесть только момент силы трения, равный
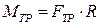 (4.2)
(4.2)
где R — радиус цилиндра. Само уравнение динамики запишем следующим образом:
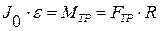 (4.3)
(4.3)
где 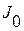 - момент инерции цилиндра,
- момент инерции цилиндра, 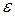 - угловое ускорение.
- угловое ускорение.
Если качение цилиндра по наклонной плоскости происходит без проскальзывания, то линейное и угловое ускорение связано соотношением:
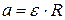
Решая совместно уравнения (4.1), (4.3) и (4.4) находим ускорение тела:
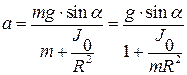 (4.5)
(4.5)
Будем считать, что цилиндр скатывается без начальной скорости с наклонной плоскости длиной 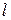 . Тогда линейная скорость центра масс в нижней точке наклонной плоскости будет равна:
. Тогда линейная скорость центра масс в нижней точке наклонной плоскости будет равна:
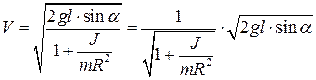 (4.6)
(4.6)
Анализируя полученное выражение для скорости тела можно убедиться в том, что при фиксированных значениях угла наклона и длины наклонной плоскости, она не зависит от массы тела, а зависит только от распределения массы относительно оси вращения. При вычислении скорости сплошного однородного цилиндра следует брать момент инерции 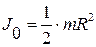 , для шара
, для шара 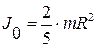 тонкостенного полого цилиндра
тонкостенного полого цилиндра 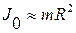 .
.
 2015-10-13
2015-10-13 5685
5685
