Мода – наиболее часто встречающееся значение признака в данном ряду.
Медиана – значение признака, делящее совокупность на две равные части по численности.
Значение моды определяется на основе полигона распределения.
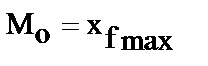 , (11)
, (11)
Ме = Хiв середине ранжированного ряда 

Показатели вариации:
- размах вариации
(именованные)
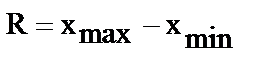 , (12)
, (12)
- среднее линейное (абсолютное) отклонение
(именованные)
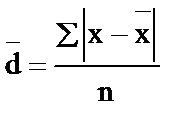 ,
, 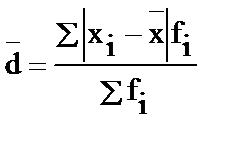 , (13)
, (13)
Таблица 1
Основные относительные величины
| 1 группа | ||
| Относительные величины выполнения плана |  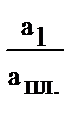
| |
| Относительные величины планового задания |  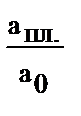
| |
| Относительные величины динамики | 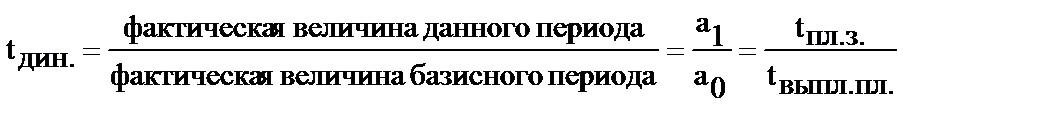
| |
| 2 группа | ||
| Относительная величина структуры Доля; Удельный вес | 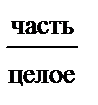
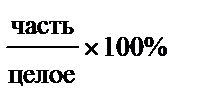
| Если есть целое, а в нем составные части |
| Относительные величины координации | 
| |
| 3 группа | ||
| Относительные величины интенсивности, в том числе относительные уровни экономического развития (плотность населения, чел/км2) | 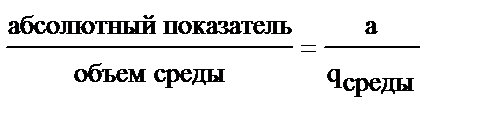
| |
| 4 группа | ||
| Относительные величины сравнения (за один и тот же период времени) |  ,
например,
Иванов в 3 раза старше Петрова ,
например,
Иванов в 3 раза старше Петрова
|
Таблица 2
Виды средних величин и условия применения
| Вид средней величины | Формула расчета |
| Средняя агрегатная (если известны числитель и знаменатель в исходной формуле) | 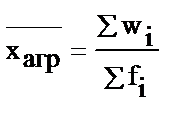
|
| Средняя арифметическая взвешенная (если неизвестен числитель в исходной формуле) | 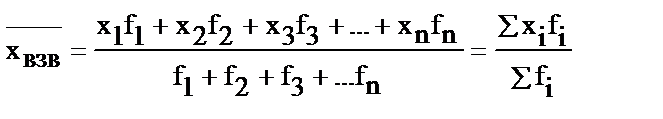
|
| Средняя арифметическая простая (если простая совокупность, т.е. есть значения, вариант - Хi) | 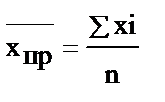
|
| Средняя гармоническая простая (если простая совокупность, т.е. есть обратные значения, вариант) | 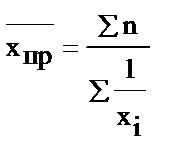
|
| Средняя гармоническая взвешенная (если неизвестен знаменатель в исходной формуле, в сложной совокупности) | 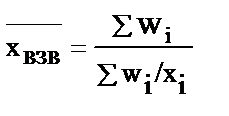
|
Окончание таблицы 2
| Средняя геометрическая (для определения среднего темпа роста) | 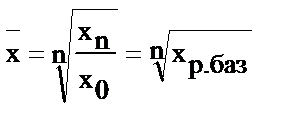
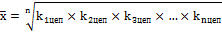
|
| Средняя хронологическая простая (для моментного ряда) с равными интервалами | 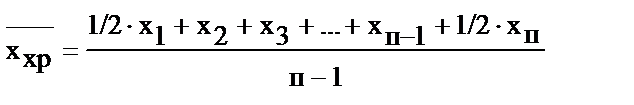
|
| Средняя хронологическая взвешенная с неравными интервалами | 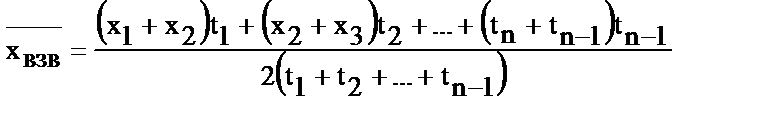
|
- среднее квадратичное отклонение
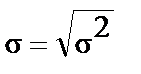 , (14)
, (14)
- дисперсия рассчитывается так:
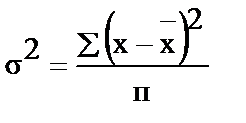
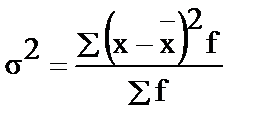
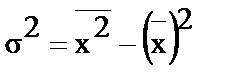 , (15)
, (15)
Общая дисперсия признака 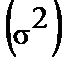 равна сумме из внутригрупповых дисперсий
равна сумме из внутригрупповых дисперсий 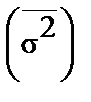 и дисперсии групповых средних
и дисперсии групповых средних 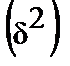
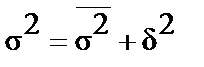 , (16)
, (16)
Относительные показатели вариации:
- коэффициенты вариации
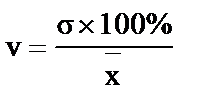 , (17)
, (17)
 2015-10-13
2015-10-13 381
381








