Середній радіус кривизни

Радіус кривизни будь-якого нормального перетину R; виражається

через головні радіуси кривизни за формулою Ейлера:

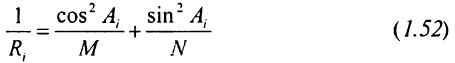
або

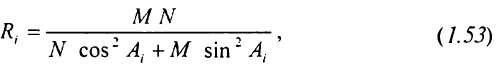
де А; - геодезичний азимут даного нормального перетину.

Середній радіус кривизни R не відноситься ні до однієї лінії на еліпсоїді. Він характеризує форму поверхні в даній точці і визначається як межа середнього арифметичного з радіусів кривизни можливих нормальних перерізів, проведених через дану точку поверхні в різних напрямках, тобто

Уявімо А як суму елементарних перетворень азимута 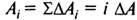, відповідно до цього для повного циклу змін азимута будемо мати 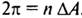Тоді (1.54) з урахуванням (1.53) прийме вигляд

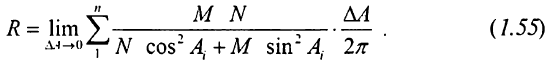
Замінюючи межа суми визначеним інтегралом, отримаємо

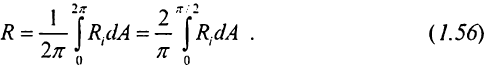
Останній інтеграл запишемо так:

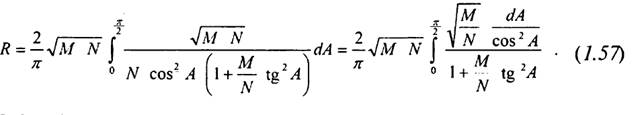
Введемо заміну змінних

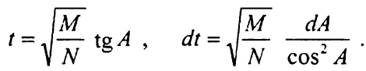
Тепер (1.57) прийме вигляд

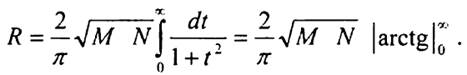
Звідси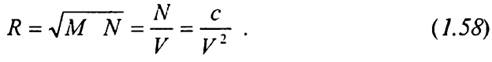

Таким чином, середній радіус кривизни обчислюється як середнє геометричне з головних радіусів кривизни. цей результат був вперше отриманий Гаусом, тому в його честь величина.