Паралель є коло радіуса, r = N cosB. позначимо довжину дуги паралелі між точками з довготами L1 і L2 через 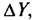 тоді, застосовуючи (1.60), одержимо
тоді, застосовуючи (1.60), одержимо 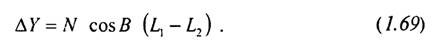
Площа сфероїдичної трапеції
Сфероїдичною трапецією називається частина поверхні еліпсоїда, обмежена меридіанами і паралелями (pиc.1.8).
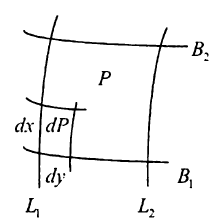
Рис.1.8. Площа сфероїдичної трапеції
Площа елементарної трапеції dP обчислюється за формулою
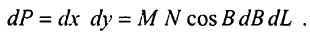
Враховується те, що
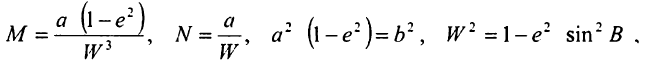
для площі сфероїдичної трапеції кінцевих розмірів отримаємо
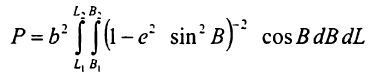
або
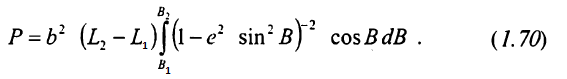
Підінтегральну функцію в (1.70) розкладемо в ряд
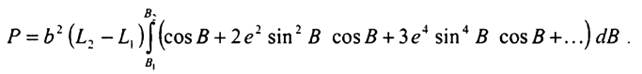
Почленною інтеграцією цього ряду отримаємо
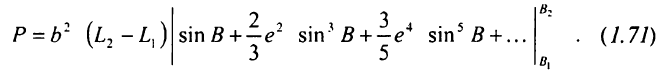
У наближених розрахунках часто використовується радіус еквівалентного кулі R, площа якого дорівнює плошали еліпсоїда, 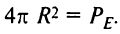 . Для обчислен-ня
. Для обчислен-ня 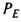 у формулі (1. 71) покладемо
у формулі (1. 71) покладемо
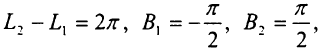
тоді
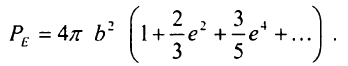
Звідси знайдемо
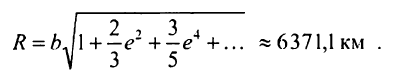
 2015-10-13
2015-10-13 846
846








