З (рис.1.12) і формул (1. 61) і (1. 69) можна отримати
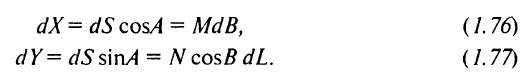
Отримані вирази справедливі для будь-якої довільної кривої. Для того щоб отримати рівняння геодезичної лінії, необхідно до рівності (1.76) і (1.77) приєднати ще одне, яке відображало б властивості, присуши тільки геодезичної лінії.
Розглянемо довільну криву на площині еліпсоїда. Якщо пересуватися уздовж цієї лінії, то в кожній її точці азимут буде змінюватися, по-перше, внаслідок зміни геодезичної кривизни, по-друге, через непаралельності меридіанів (явище зближення меридіанів). На рис. 1.13 зображений елементарний полярний сферичний прямокутний трикутник Q3Q2P. Застосовуючи до нього правило Непера 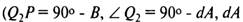 - кут між меридіанами Q1P і Q2P), отримаємо
- кут між меридіанами Q1P і Q2P), отримаємо
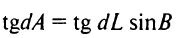
або, замінюючи тангенси малих кутів самими кутами,

Оскільки для геодезичної лінії геодезична кривизна усюди дорівнює нулю і, отже, змін азимута через неї не виникає, то вираз (1.78) і буде диференціальним рівнянням, властивим тільки геодезичної лінії. Приєднавши до нього виразу (1.76) і (1.77), отримаємо систему диференціальних рівнянь геодезичної лінії
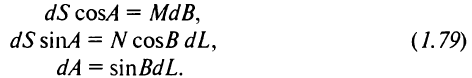
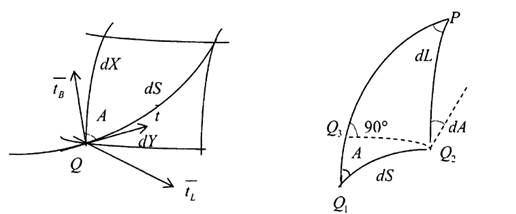
Рис. 1.12. Диференціальні елементи кривої на поверхні еліпсоїда
Рис. 1.13. Зміна азимута геодезичної лінії
Висновок диференціального рівняння (1.78) заснований на найпростіших геометричних уявлень і, на перший погляд, може здатися не цілком коректним. Тому наведемо традиційний висновок цього рівняння з використанням строгих формул Серрі-Френе.
Попередньо встановимо деякі співвідношення для координатних ліній на поверхні еліпсоїда. Крім того, нагадаємо, що по одному з визначень для геодезичної лінії, її головна нормаль 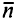 в кожній точці збігається з нормаллю до поверхні
в кожній точці збігається з нормаллю до поверхні 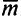 .
.
Запишемо рівняння Серрі-Френе (1.1) для меридіана і паралелі. Кривизна меридіана дорівнює 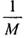 , паралелі
, паралелі 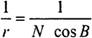 . Обидві криві плоскі, тому їх кручення дорівнює нулю.
. Обидві криві плоскі, тому їх кручення дорівнює нулю.
Для меридіана будемо мати 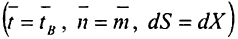
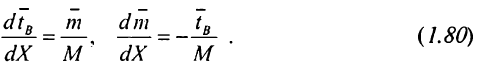
Для паралелі 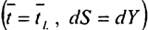 отримаємо
отримаємо

Спроектуємо паралель на дотичну площину, в результаті отримаємо криву, яку позначимо через Sk. Кривизна цієї кривої буде (див. Puc.1.6)

Формули Серрі-Френе для лінії Sk запишуться 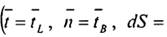
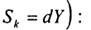
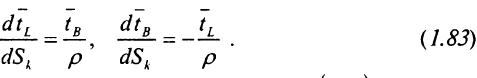
Складемо скалярну похідну (див. Puc.1.12) 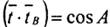 продиференціюємо її по S:
продиференціюємо її по S:
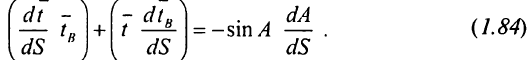
Знайдемо похідні, що входять у вираз (1.84). Для геодезичної лінії 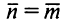 , тому, згідно першому рівнянню (1.1), отримаємо
, тому, згідно першому рівнянню (1.1), отримаємо

Похідна одиничного вектора 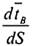 розкладемо на дві складові: в площині меридіана і в дотичній площині
розкладемо на дві складові: в площині меридіана і в дотичній площині
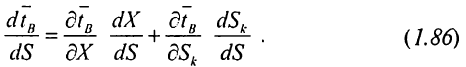
Перші співмножники у формулі (1.86) визначимо з виразів (1.80) і (1.83), другі, відповідно до (1. 76) і (1.77), мають вигляд
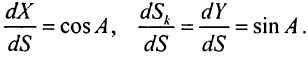
Виконавши ці заміни, для вираження (1.86) отримаємо
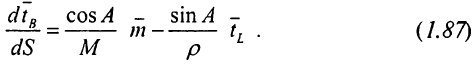
Підставами (1.87) в (1.84) і врахуємо, що
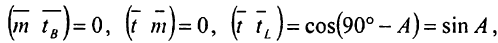
тоді, після зі фарбування лівої і правої частин рівності (1.84) на sinA, матимемо

або з урахуванням (1.82)

З виразу (1. 77) знайдемо 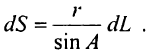
Підставляючи цей результат у формулу (1.89), остаточно отримаємо
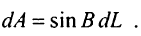
Таким чином, ми знову прийшли до рівняння (1.78), що й підтверджує коректність першого, безумовно більш простого, виводу.
 2015-10-13
2015-10-13 977
977








