Состоятельные и несмещенные оценки основных параметров распределения случайной величины Х (илиY) математического ожидания mх (или mY) и дисперсии 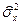 (или
(или 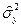 ) могут быть получены по формулам:
) могут быть получены по формулам:
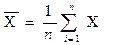 ; (3.1)
; (3.1)
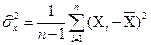 , (3.2)
, (3.2)
где n — число, определяющее размер выборки.
Оценку коэффициента корреляции между величинами Х и Y определяют по формуле:
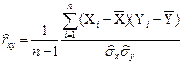 (3.3)
(3.3)
Коэффициент корреляции показывает степень связи между переменными величинами. Если r=0, то переменные не коррелируют, а при r=±1 между переменными имеется связь.
Значения 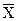 и
и 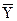 рассчитываются по формуле (3.1), а
рассчитываются по формуле (3.1), а 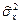 и
и 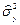 — по формуле (3.2).
— по формуле (3.2).
Так как оценки (3.1) — (3.3) определяют по выборке конечного размера, возникает вопрос об их статистической достоверности и точности.
Обозначим через 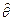 оценку интересующего нас параметра. Тогда задача определения достоверности и точности оценки сводится к определению такого интервала (q1, q2), включающего параметр qкр, что с вероятностью 1-p (р – уровень значимости, достаточно малая величина, равная 0,1; 0,05; 0,01) можно утверждать, что неизвестное истинное значение параметра находится в этом интервале. Интервал (q1, q2) называют доверительным интервалом, а вероятность 1-р — доверительной вероятностью.
оценку интересующего нас параметра. Тогда задача определения достоверности и точности оценки сводится к определению такого интервала (q1, q2), включающего параметр qкр, что с вероятностью 1-p (р – уровень значимости, достаточно малая величина, равная 0,1; 0,05; 0,01) можно утверждать, что неизвестное истинное значение параметра находится в этом интервале. Интервал (q1, q2) называют доверительным интервалом, а вероятность 1-р — доверительной вероятностью.
Рассмотрим случай, когда величина Х (и Y) имеет нормальный закон распределения с плотностью вероятности
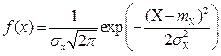 .
.
Здесь и далее во всех формулах величины Х можно заменить на Y.
Доверительный интервал для математического ожидания (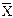 -ep,
-ep, 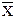 +ep), включающий m х с вероятностью 1-р, находят из условия
+ep), включающий m х с вероятностью 1-р, находят из условия
P[ 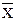 -ep<mx<
-ep<mx< 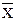 +ep]=1-p,
+ep]=1-p,
которое можно представить в виде
P[| 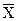 -mx|<ep]=1-p. (3.4)
-mx|<ep]=1-p. (3.4)
Введем параметр t=[(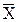 -mx)/
-mx)/ 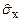 ]×
]× 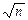 , имеющий t-распределение Стьюдента с f = n-1 степенями свободы. Тогда равенство (3.4) перепишется в виде:
, имеющий t-распределение Стьюдента с f = n-1 степенями свободы. Тогда равенство (3.4) перепишется в виде:
P[ | 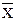 -mx|<t(p,f)
-mx|<t(p,f) 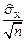 ]=1-p,
]=1-p,
где t(p,f) определяют по таблице распределения Стьюдента (табл. 3.1) при вероятности р и числе степеней свободы f = n-1. Доверительный интервал для mx, соответствующий доверительной вероятности 1-р, есть
[ 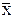 -t(p,f)
-t(p,f) 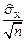 ,
, 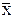 +t(p,f)
+t(p,f) 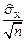 ]. (3.5)
]. (3.5)
Чтобы определить доверительный интервал для генеральной дисперсии, необходимо найти границы интервала 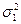 и
и 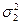 , удовлетворяющие равенству
, удовлетворяющие равенству
P[ 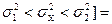 1-p. (3.6)
1-p. (3.6)
Для нормально распределенного Х известен закон распределения величины
 (3.7)
(3.7)
который называют χ2-распределением Пирсона с f = n-1 степенями свободы. После подстановки соотношения (3.7) в (3.6) при условии, что
P[ 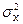 <
< 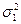 ]=P[
]=P[ 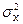 >
> 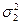 ]=p2,
]=p2,
Получим
[χ2 (p/2,f)≤ 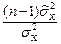 ≤χ2(1-p/2,f)]=1-p.
≤χ2(1-p/2,f)]=1-p.
Величину χ2(1-p/2,f)=(n-1) 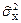 /
/ 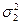 находят по таблице 3.2 χ2 распределения при вероятности 1-р/2 и числе степеней свободы f = n-1, а χ2(p/2,f)=(n-1)
находят по таблице 3.2 χ2 распределения при вероятности 1-р/2 и числе степеней свободы f = n-1, а χ2(p/2,f)=(n-1) 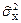 /
/ 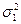 определяют по таблице 3.2 при вероятности р/2 и числе степеней свободы f = n-1. Следовательно, доверительный интервал для дисперсии
определяют по таблице 3.2 при вероятности р/2 и числе степеней свободы f = n-1. Следовательно, доверительный интервал для дисперсии 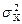 , соответствующий доверительной вероятности, есть
, соответствующий доверительной вероятности, есть
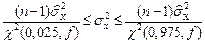 . (3.8)
. (3.8)
Величина 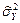 находится аналогично
находится аналогично 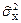 .
.
 2015-10-13
2015-10-13 335
335








