2015-10-13
3072
Для вычисления приближенных значений параметров чаще всего применяются методы моментов и максимального правдоподобия.
Суть метода моментов заключается в следующем. Пусть имеется выборка { x 1,..., xn } независимых значений случайной величины с известным законом распределения f (x, Q 1,..., Qm) и m неизвестными параметрами Q 1,..., Qm. Последовательность вычислений следующая.
1. Вычислить значения m начальных и/или центральных теоретических моментов
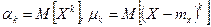. (6.12)
2. Определить m соответствующих выборочных начальных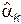 
и/или центральных 
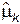моментов по формулам (6.8, 6.9).
3. Составить и решить систему из m уравнений, в каждом из которых приравниваются теоретические и выборочные моменты. Каждое уравнение имеет вид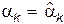 
или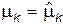 
.
Замечание. Часть уравнений может содержать начальные моменты, а оставшаяся часть - центральные.
Согласно методу максимального правдоподобия оценки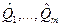 
получаются из условия максимума по параметрам Q 1,..., Qm положительной функции правдоподобия L (x 1,..., xn, Q 1,..., Qm).
Если случайная величина X - непрерывна, а значения xi независимы, то
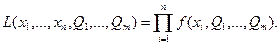(6.13)
Если случайная величина X - дискретна и принимает независимые значения xi с вероятностями
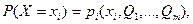(6.14)
то функция правдоподобия равна
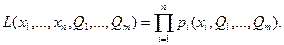(6.15)
Система уравнений согласно этому методу может записываться в двух видах:
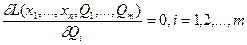(6.16)
или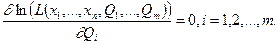 
(6.17)
Пример 6.1. Пусть xi - независимые значения случайной величины X, распределенной по экспоненциальному закону, т.е.
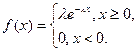
Необходимо получить оценку параметра методом максимального правдоподобия.
Решение. Функция правдоподобия имеет вид
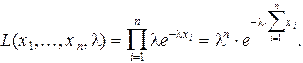
Тогда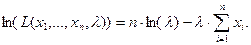 
Далее записываем уравнение
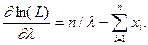=0.
Отсюда получаем выражение для оценки параметра:
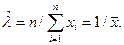
Пример 6.2. Случайная величина X распределена по равномерному закону, т.е.
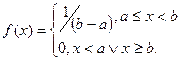
Необходимо определить оценки параметров a и b.
Решение. Составляем систему их 2-х уравнений: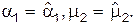 
Здесь
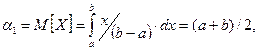
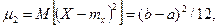
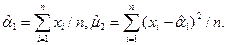
Подставив данные выражения в систему и решив ее, получим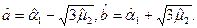 
ЗАДАЧИ
6.1. Имеется выборка объема n: x 1,..., xn из генеральной совокупности, распределенной по закону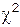 
с неизвестным параметром, т.е. с плотностью 
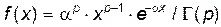(x >0). Найти методом наибольшего правдоподобия оценку параметра.
Ответ: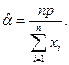 
6.2. Найти методом моментов по известной выборке x 1,..., xn оценку параметра Q случайной величины с плотностью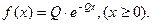 
.
Ответ: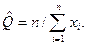 
6.3. Отобрано 5 телевизоров для контроля некоторых параметров. Результаты измерения напряжения источника питания в телевизорах: 12; 11,5; 12,2; 12,5; 12,3 В. Методом наибольшего правдоподобия найти оценку параметра m, если напряжение - случайная величина X, распределенная по нормальному закону.
Ответ: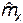 
= 12,1 В.
6.4. Отобраны случайно 200 однотипных радиостанций. Время их работы до первого отказа характеризуется таблицей
| Срок службы, ч | 900-1100 | 1100-1300 | 1300-1500 |
К-во радиостанций,  i |
Вычислить выборочное среднее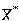 
, дисперсию 
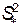, и среднее квадратическое отклонение S* срока службы радиостанций до первого отказа.
Примечание. Если отдельные значения в ряде распределения повторяются по нескольку раз, то следует учесть частоту каждого повторения. Тогда выборочное среднее и дисперсию вычисляют по формулам
,
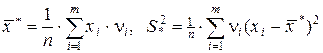где xi -среднее значение X в i -том интервале;
i- количество значений, попавших в i -тый интервал;
m - количество интервалов.
Ответ: 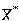=1260 ч, 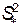=12400 ч2, 
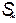=111.4 ч.
6.5. Определить методом наибольшего правдоподобия оценку параметра p биномиального распределения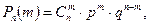 
если в n 1независимых опытах событие A появилось m 1раз и в n 2независимых опытах - m 2раз.
Ответ: p = (m 1 + m 2)/(n 1 + n 2).
