При расчёте кривой свободной поверхности по методу Бахметева её длина определяется по уравнению неравномерного движения (уравнению Бахметева).
Для случая 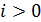 уравнение имеет вид:
уравнение имеет вид:
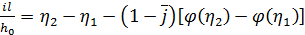 , (1.7)
, (1.7)
где 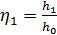 ,
, 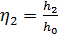 – относительные глубины в расчётных сечениях;
– относительные глубины в расчётных сечениях;
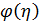 - функция определяемая по таблице из справочной литературы;
- функция определяемая по таблице из справочной литературы;
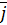 - среднее для рассматриваемого участка значение величины
- среднее для рассматриваемого участка значение величины 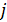 .
.
Величину 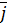 рассчитываем по формуле
рассчитываем по формуле 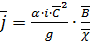 , в которой
, в которой 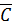 ,
, 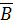 ,
, 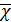 вычисляем для средней глубины
вычисляем для средней глубины 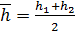 .
.
Принимаем: 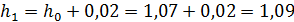 м,
м, 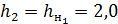 м.
м.
Вычислим 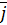 :
:
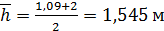 ;
;
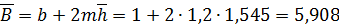 м;
м;
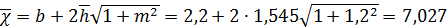 м;
м;
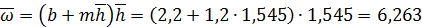 м2;
м2;
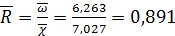 м;
м;
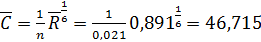 м0,5/с;
м0,5/с;
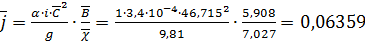 ,
,
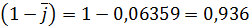 .
.
Расчёт 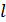 для каждого участка выполняем в табличной форме (Таблица 1.7).
для каждого участка выполняем в табличной форме (Таблица 1.7).
Таблица 1.7 – К расчёту кривой свободной поверхности
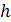 , м , м | 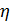 | 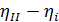 | 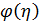 | 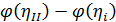 | 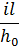 | 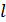 , м , м |
| 1,090 | 1,019 | 0,850 | 0,798 | – 0,740 | 1,54264 | 4945,522 |
| 1,181 | 1,104 | 0,765 | 0,395 | – 0,337 | 1,080432 | 3463,738 |
| 1,272 | 1,189 | 0,680 | 0,272 | – 0,214 | 0,880304 | 2822,151 |
| 1,363 | 1,274 | 0,595 | 0,204 | – 0,146 | 0,731656 | 2345,603 |
| 1,454 | 1,359 | 0,510 | 0,160 | – 0,102 | 0,605472 | 1941,072 |
| 1,545 | 1,444 | 0,425 | 0,129 | – 0,071 | 0,491456 | 1575,55 |
| 1,636 | 1,529 | 0,340 | 0,107 | – 0,049 | 0,385864 | 1237,035 |
| 1,727 | 1,614 | 0,255 | 0,089 | – 0,031 | 0,284016 | 910,522 |
| 1,818 | 1,699 | 0,170 | 0,076 | – 0,018 | 0,186848 | 599,013 |
| 1,909 | 1,784 | 0,085 | 0,065 | – 0,007 | 0,091552 | 293,505 |
| 2,000 | 1,869 | 0,058 |
 2015-10-14
2015-10-14 776
776








