В зависимости от гидравлических условий, создающихся при возведении сооружений, и состояния потока глубины по его длине могут увеличиваться (кривая подпора) или уменьшаться (кривая спада).
Форма кривой свободной поверхности устанавливается на основе анализа дифференциального уравнения неравномерного движения третьего вида
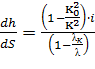 , (1.4)
, (1.4)
где 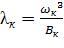 ,
, 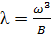 .
.
При этом тип кривой свободной поверхности зависит от зоны, в которой находится фиксируемая глубина 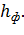
Равенство числителя нулю в уравнении (1.4), когда 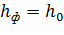 и при этом
и при этом 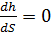 , соответствует равномерному движению. Если знаменатель стремится к нулю, то
, соответствует равномерному движению. Если знаменатель стремится к нулю, то 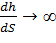 и свободная поверхность скачкообразно повышается (или понижается). В первом случае происходит переход потока из бурного состояния в спокойное – так называемый гидравлический прыжок, во втором – образуется водопад.
и свободная поверхность скачкообразно повышается (или понижается). В первом случае происходит переход потока из бурного состояния в спокойное – так называемый гидравлический прыжок, во втором – образуется водопад.
Когда числитель и знаменатель не равны 0, возможны различные сочетания знаков числителя и знаменателя. При 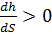 глубина вдоль потока непрерывно и плавно увеличивается (кривая подпора), а при
глубина вдоль потока непрерывно и плавно увеличивается (кривая подпора), а при 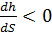 непрерывно и плавно уменьшается (кривая спада).
непрерывно и плавно уменьшается (кривая спада).
При неравномерном движении в русле с прямым уклоном (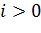 ) различают три случая, характеризуемыми условиями:
) различают три случая, характеризуемыми условиями:
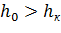 и
и 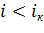 .
.
При этом получаем три возможные формы кривой свободной поверхности: кривые подпора 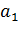 ,
, 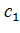 и кривую спада
и кривую спада 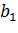 .
.
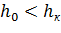 и
и 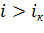 .
.
Здесь также получаем три возможные формы кривой свободной поверхности: кривые подпора 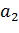 ,
, 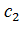 и кривую спада
и кривую спада 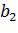 .
.
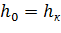 и
и 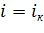 .
.
Здесь получаем две возможные формы кривой свободной поверхности - кривые подпора 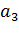 ,
, 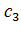 . В случае широкого прямоугольного русла, если считать, что коэффициент Шези
. В случае широкого прямоугольного русла, если считать, что коэффициент Шези 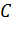 не изменяется с глубиной (
не изменяется с глубиной (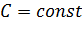 ), кривые подпора превращаются в прямые горизонтальные линии.
), кривые подпора превращаются в прямые горизонтальные линии.
Таким образом, вопрос о форме свободной поверхности решаем путём сопоставления фактической глубины потока 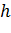 с глубинами
с глубинами 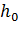 и
и 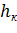 :
:
В нашем случае 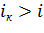 и
и 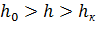 , значит в русле образуется кривая спада типа
, значит в русле образуется кривая спада типа 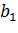 .
.
 2015-10-14
2015-10-14 942
942








