Краткое содержание темы

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Определение 1: Отличающиеся друг от друга порядком наборы, составленные из всех элементов данного конечного множества, называются перестановками этого множества.

Пример 1. Множество, состоящее из трех элементов {1,2,3}, имеет следующие перестановки: (1,2,3), (1,3,2), (2,3,1), (2,1,3), (3,2,1), (3,1,2). Число всех перестановок множества из n элементов обозначается Рn.

Теорема 1: (о числе перестановок). Число перестановок Рn определяется по формуле:

Рn = n!, где n! = 1 • 2 • 3 •... • n.

Задача 1: Сколькими различными маршрутами можно навестить больного по 5 адресам?

Решение: Занумеруем адреса цифрами от 1 до 5. Каждому маршруту можно сопоставить один из наборов, со­стоящих из этих пяти цифр, например, (2,5,3,4,1). Такой набор означает, что сначала выбирается второй адрес, затем пятый, третий, четвертый и первый. Всего различных маршрутов, т. е. отличающихся порядком наборов пяти цифр будет
5! = 120.

Определение 2: Упорядоченные наборы, состоящие из k различных элементов, выбранных из данных n элементов, называются размещениями из n элементов по k.

Размещения могут отличаться друг от друга как элементами, так и порядком.

Пример 2. Различными размещениями множества из трех элементов {1,2,3} по два будут наборы (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).

Число всех размещений из n элементов по k обозначается. .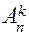

При k = п число размещений совпадает с числом перестановок.

Теорема 2 (о числе размещений). Число размещений из n элементов по k определяется по формуле

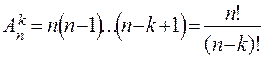
Задача 2: Студентам надо сдать 4 экзамена за 8 дней. Сколькими способами можно составить расписание сдачи экзаменов

Решение. Занумеруем дни сдачи экзаменов цифрами 1,2,...,8. Составлять различные расписания можно следую­щим образом. Сначала выберем дни для сдачи экзаменов, например, (2,4,5,7), а затем порядок сдачи экзаменов. Таким образом, нужно составить различные наборы четырех чисел из восьми, которые отличаются друг от друга не только элементами, но и порядком. Таких наборов 4: 8* 7 *6*5 = 1680.

Определение 3: Неупорядоченные наборы, состоящие из k элементов, взятых из данных п элементов, называются сочетаниями
из n элементов по k.

Сочетания отличаются друг от друга только элементами.

Пример 3. Для множества {1,2,3} сочетаниями по 2 элемента являются {1, 2}, {1, 3}, {2, 3}.

Число всех сочетаний из п элементов по k обозначается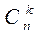

Теорема 3 (о числе сочетаний). Число сочетаний из n элементов по k определяется по формуле

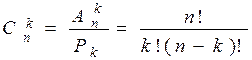
Задача 3: В хоккейном турнире участвуют 6 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире?

Решение. Различные пары команд образуют сочетания из б по 2, поскольку порядок среди двух команд, играющих в одной игре, нам безразличен. Следовательно, число игр будет равно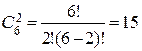

Вероятность события А:
Р (А)= 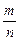, где m – число благоприятных исходов, n – число всех исходов.

X – величина, Р – вероятность.

Такую таблицу называют законом распределения дискретной случайной величины.