Будь-яка просторова система сил приводиться до однієї сили - головного вектора 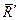 - та однієї пари сил, момент якої дорівнює головному моменту
- та однієї пари сил, момент якої дорівнює головному моменту 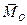 . Можливі такі випадки:
. Можливі такі випадки:
а) для даної системи сил головний вектор 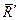 і головний момент
і головний момент 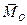 дорівнюють нулю (
дорівнюють нулю (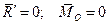 ) - система знаходиться в рівновазі. При цьому діючі сили задовольняють умовам рівнянь (8.14) і (8.15);
) - система знаходиться в рівновазі. При цьому діючі сили задовольняють умовам рівнянь (8.14) і (8.15);
б) якщо для даної системи сил 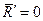 , а
, а 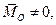 то система приводиться до пари сил, момент якої обчислюється за допомогою формул (8.7) і (8.8). Напрямні косинуси вектора
то система приводиться до пари сил, момент якої обчислюється за допомогою формул (8.7) і (8.8). Напрямні косинуси вектора 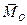 визначаються за формулами (8.9);
визначаються за формулами (8.9);
в) якщо для даної системи сил 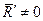 , а
, а 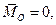 то система приводиться до рівнодіючої
то система приводиться до рівнодіючої 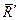 , яка проходить через центр приведення О та обчислюється за допомогою формул (8.4), (8.5), (8.6);
, яка проходить через центр приведення О та обчислюється за допомогою формул (8.4), (8.5), (8.6);
 г) якщо для даної системи сил
г) якщо для даної системи сил 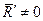 і
і 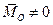 , але
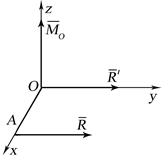
, але 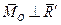 (рис. 8.4), то ця система сил також приводиться до однієї рівнодіючої, яка дорівнює
(рис. 8.4), то ця система сил також приводиться до однієї рівнодіючої, яка дорівнює 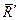 і прикладена в точці А.
і прикладена в точці А.
Відстань ОА обчислюється за формулою:

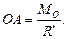 (8.16)
(8.16)
Вектор 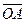 направлений так, щоб обертання навколо точки О силою
направлений так, щоб обертання навколо точки О силою 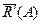 відбувалось проти ходу годинникової стрілки;
відбувалось проти ходу годинникової стрілки;
д) якщо для даної системи сил 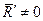 і
і 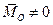 , а
, а 
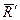 II
II 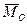 (рис. 8.5 а), то система сил приводиться до однієї сили
(рис. 8.5 а), то система сил приводиться до однієї сили 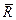
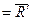 і пари сил
і пари сил 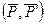 , яка лежить у площині, перпендикулярній до сили
, яка лежить у площині, перпендикулярній до сили 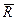 . Така сукупність сили та пари сил називається динамічним гвинтом або динамою. Пряма, уздовж якої направлений вектор
. Така сукупність сили та пари сил називається динамічним гвинтом або динамою. Пряма, уздовж якої направлений вектор 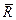 , називається віссю динами (рис. 8.5 б);
, називається віссю динами (рис. 8.5 б);
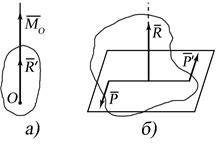
 е) якщо для даної системи сил
е) якщо для даної системи сил 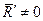 ,
, 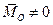 і
і 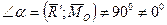 , то така система сил також приводиться до динами, але вісь динами не проходить через точку О, а проходить через точку А (рис. 8.6 а, б). При цьому:
, то така система сил також приводиться до динами, але вісь динами не проходить через точку О, а проходить через точку А (рис. 8.6 а, б). При цьому:
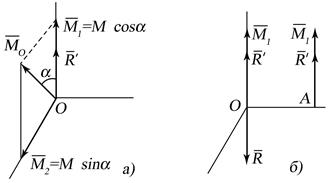
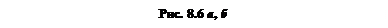
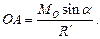 (8.17)
(8.17)
Рівняння центральної гвинтової осі мають вигляд:
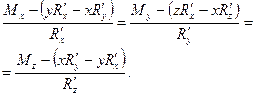 (8.18)
(8.18)
Вказівка. Для закріплення теоретичного матеріалу § 8 необхідно розв’язати наступні задачі із збірника: Мещерский И.В. Сборник задач по теоретической механике. - М.: Наука, 1981 (або 1986):
1) №№ 8.12 - 8.16;
2) №№ 8.17; 8.19; 8.21; 8.24; 8.28; 8.36;
3) №№ 8.31; 8.33; 8.37 - 8.39.
 2015-10-14
2015-10-14 555
555








