При построении теории пьезоэлектрического преобразователя уравнения Максвелла используются в следующем виде:
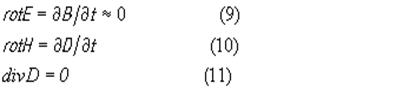
Первое из этих уравнений означает, что теория строится в квазистатическом приближении. Для обоснования этого можно привести следующие соображения. Электрические поля, порождаемые в пьезоэлектрике упругой волной возникают благодаря перераспределению этой волной положительных и отрицательных зарядов в объеме среды. Созданный при этом зарядовый “рельеф” переносится упругой волной со скоростью звука. Последняя в ≈105 раз меньше скорости распространения электромагнитных волн. Поэтому указанные заряды можно считать неподвижными, а электрические поля, создаваемые ими - потенциальными, подчиняющимися законам электростатики.
В уравнении (10) отсутствует плотность тока проводимости и оставлена только плотность тока смещения ∂ D/dt. Это связано с тем, что пьезоэлектрик, используемый в электроакустическом преобразователе, должен быть непроводящим. В противном случае он будет шунтироваться собственной проводимостью, которая снизит в нем амплитуду переменного поля. Равенство нулю дивергенции в (11) следует из того, что пьезоэлектрик считается непроводящим и плотность объемного заряда в нем равна нулю.
2.4. Волновое уравнение для плоских ОАВ в пьезоэлектрике. Рассмотрим случай, когда в переменное электрическое поле введен конец пьезоэлектрического звукопровода, либо пьезоэлектрическая пластина,
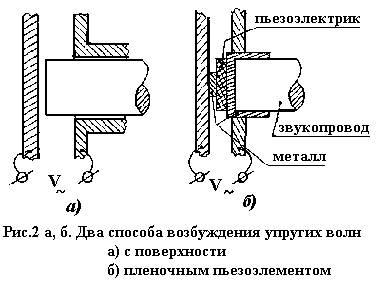
закрепленная на непьезоэлектрическом звукопроводе (см.рис.2). Предположим, что пьезокристалл ориентирован осью x 3 кристаллофизической системы координат параллельно вектору электрического поля, а его торцевая поверхность перпендикулярна этой оси. В таком случае в пьезоэлектрике будут возбуждаться практически плоские ОАВ с фазовой скоростью, направленной вдоль оси x 3 и можно положить ∂/ dx 1 =∂ /dx 2 =O. Уравнения (5), (6), (8), (11) с учетом (7) примут вид
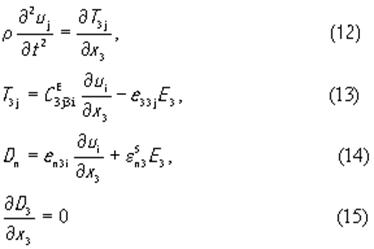
Из последнего уравнения следует, что D3 не зависит от координаты x3 и, следовательно, является лишь функцией времени. Выразим из (14) напряженность электрического поля E 3
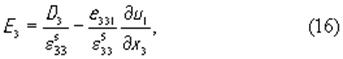
подставим ее в (13)
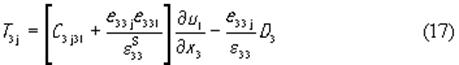
и, используя полученное выражение, найдем из (12) следующее волновое уравнение.
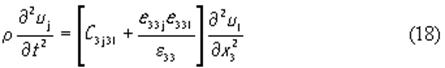
Поскольку j здесь может принимать значения 1,2,3, формула (18) представляет собой три уравнения, в которых неизвестными служат компоненты вектора смещения uj (x3, t).
Рассмотрим случай, когда пьезоэлектриком является кристалл класса 6mm, например, ZnO или CdS. Если воспользоваться матрицами упругих, пьезоэлектрических и диэлектрических постоянных для таких кристаллов [4], то нетрудно убедиться, что во всех приведенных выше уравнениях неравными нулю будут только константы C3131 = C3232 , C3333 , e333 и ε33. Тогда из (13) и (14) будем иметь
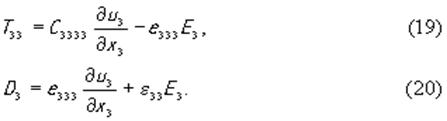 а из (18) получим
а из (18) получим
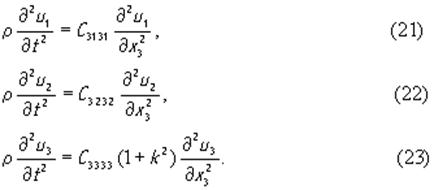
В последнем уравнении величина k = (e 2333 / C 3333 ε33)1/2 
называется коэффициентом электромеханической связи. Таким образом, в пьезоэлектрике класса 6mm в направлении оси x 3 возможно распространение двух чисто поперечных волн со смещениями вдоль x 1 и x 2 (см.(21) и (22)) и чисто продольной волны со смещением вдоль оси x3 (см.(23)). Скорости этих волн, как следует из дисперсионных уравнений, которые нетрудно получить из (21), (22) и (23), соответственно, равны (C 3131/ρ)1/2 , (C 3232/ρ)1/2 и (C3333 (1 +k2)/ρ)1/2. Заметим, что обе поперечные волны имеют одинаковые скорости, так как C 3131 = C 3232. Переменным электрическим полем, направленным вдоль оси x 3, будет возбуждаться лишь одна из этих трех волн, а именно продольная волна. Действительно, если в (12) подставить (13) и воспользоваться матрицами материальных констант [4], то из трех уравнений, которые мы при этом получим, два точно совпадают с (21) и (22), а третье примет вид
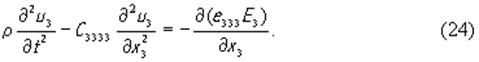
Правая часть этого неоднородного уравнения представляет в нем источник возбуждения акустических волн. Следовательно, для возбуждения упругой волны в пьезоэлектрике необходимо, чтобы производная ∂(e333E3)/∂x3 была бы отлична от нуля, т.е. произведение (e333E3) должно изменяться в зависимости от координаты x3. Если, например, плоская граница пьезоэлектрика перпендикулярна оси, то значение e333 испытывает на ней скачок и будет иметь место так называемое “возбуждение с поверхности”.В случае пьезоэлектрика класса 6mm возможен также другой случай, когда переменное электрическое поле, направленное перпендикулярно торцу звукопровода, возбуждает чисто поперечную волну. Для этого необходимо сориентировать пьезоэлектрик таким образом, чтобы ось x3 кристаллофизической системы координат оказалась бы перпендикулярной вектору электрического поля E и, следовательно, параллельной собственному торцу кристалла. В этом случае чисто поперечная волна может возбуждаться в любом направлении, лежащем в плоскости x 1 O x 2. Например, для волн, распространяющихся вдоль оси x1, тензорные уравнения (5), (6) и (8) сводятся к следующим скалярным
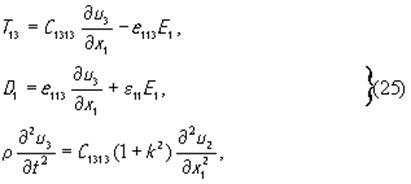
где k - коэффициент электромеханической связи, равный

Решением уравнения (25) является чисто поперечная волна, распространяющаяся вдоль оси x1 со смещением частиц среды параллельно оси x3. Две другие волны, существование которых также возможно, не возбуждаются при заданном направлении электрического поля. Таким образом, в рассмотренных двух случаях тензорные уравнения, описывающие электромеханические свойства пьезоэлектрика, сводятся к скалярным. Обобщая оба случая, будем в дальнейшем необходимые нам уравнения записывать, опуская индексы, в следующем виде
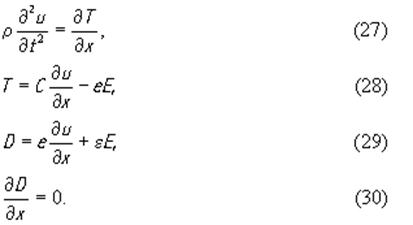
 2015-04-01
2015-04-01 778
778








