Две случайные величины х и у находятся в корреляционной зависимости, если изменение одной из величин влечет за собой изменение закона распределения другой. Для характеристики зависимости между случайными величинами вводят понятие корреляционного момента или ковариации. Корреляционным моментом случайной величины х и у называется математическое ожидание произведения отклонений этих величин от их математических ожиданий
Корреляционные зависимости
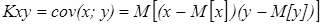 ,
,
Для дискретной случайной величины (отношение) ковариация вычисляется
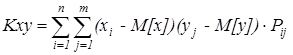 (1)
(1)
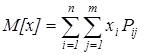 (2)
(2) 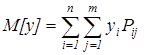 (3)
(3)
Для непрерывных случайных величин
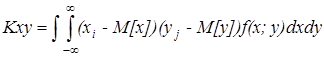 (4)
(4)
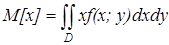 (5)
(5)
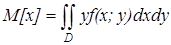 (6)
(6)
Из формулы (4) можно получить более простую формулу.
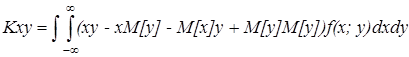
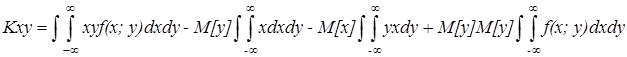
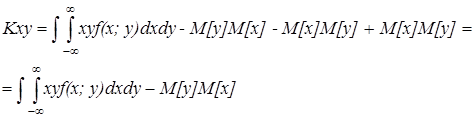
Получим
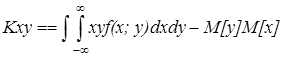 (7)
(7)
Теорема №1 Если случайные величины х и у независимы то их cov(x;y)= 0
Доказательство: для непрерывной величины.
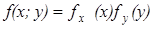
в формуле 4 заменим
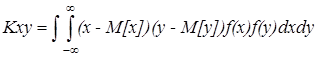
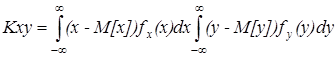
центральный момент первого порядка равен нулю, следовательно и выражение равно нулю. Для независимых случайных величин необходимо чтобы cov =0, но обратно не верно.
Если ковариация двух случайных величин отлична от нуля - это есть признак зависимости между ними. cov характеризует не только зависимость величинами, но и их рассеивание. Если одна из величин весьма мало отклоняется от своего математического ожидания, то есть почти неслучайно, то cov – будет мала, какой бы тесной зависимостью не были бы связаны эти величины. Поэтому между случайными величинами вводят безразмерный коэффициент корреляции.
Коэффициентом корреляции случайных величин х и у называется отношение их ковариации к произведению средних квадратических отклонений их величин. Корреляция - есть безразмерная величина. Поэтому величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин(в этом состоит преимущество коэффициента перед ковариацией).
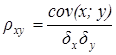 .
.
Свойства коэффициента корреляции:
1. Коэффициент корреляции независимых случайных величин равен нулю.
Это свойство вытекает из определения коэффициента корреляции. Таким образом, т.к. из независимости случайных величин следует их некоррелированность, то отличие коэффициента корреляции от нуля свидетельствует о наличии зависимости между величинами.
Как же именно коэффициент корреляции характеризует зависимость между случайными величинами?
Оказывается, что коэффициент корреляции является мерой линейной зависимости между величинами (говорят также, мерой прямолинейности):показывает, насколько хорошо в среднем может быть представлена каждая из величин в виде линейной функции от другой. Это видно из следующих свойств коэффициента корреляции.
2. Для любых величин 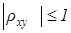
Доказательство:
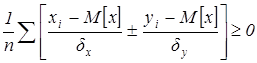 ,
,
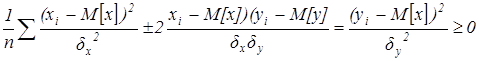 ,
,
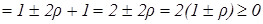 ,
,
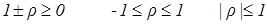 .
.
3. Если коэффициент корреляции положительный, то связь между переменными также положительна и значение переменной увеличивается и уменьшается одновременно.
Если r - имеет отрицательное значение, то при уменьшении одной переменной уменьшаются и другие.
4. Коэффициент корреляции не зависит от выбора начала отсчета и единицы измерения, то есть от любых постоянных а 1 b 1, а 2 b 2.
r(а1х+b1;a2x+b2)=r(x;y) a1,a2>0, таким образом переменные х и у можно уменьшать или увеличивать в а -раз, а также вычитать и прибавлять одно и тоже число b, в результате величина коэффициента корреляции не изменяется.
5. Если случайные величины х и у линейно зависимы, т.е. существует между ними соотношения у=ах+b, то |rху|= 1
Пример: Дана таблица, закон распределения двумерной случайной величины
| у\х | 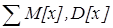 , , 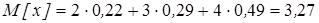 , , 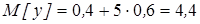 , , | |||
| 0,12 | 0,18 | 0,1 | ||
| 0,1 | 0,11 | 0,39 |
D[x]=M[x2]-M2[x]
Вывод: коэффициент корреляции есть показатель того, насколько связь между случайными величинами близка и строгой линейной зависимости.
Он отмечает и слишком большую долю случайности. Существуют также случайные величины, для которых коэффициент корреляции является достаточно полным показателем зависимости. Сюда относятся в первую очередь величины, между которыми заранее, из общих соображений, можно предсказать линейную зависимость.
Например: измеряя в электрической цепи одновременно напряжение и силу тока, мы (по закону Ома) должны ожидать между ними линейной зависимости (пропорциональности). Поэтому сильное отличие коэффициента корреляции от 1 будет свидетельствовать о недостатках измерительных приборов или о наличии переменного сопротивления в цепи.
Сильно повышается ценность коэффициента корреляции для величин, собственные случайные колебания которых подчиняются нормальному закону. Для таких величин равенство коэффициента корреляции нулю означает отсутствие всякой зависимости.
Последнее свойство особенно важно, т.к. при обработке наблюдений преимущественно сталкиваемся с нормальным распределением.
 2014-01-25
2014-01-25 2193
2193
