Пусть функция  имеет производную
имеет производную 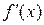 в каждой точке
в каждой точке 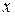 некоторого множества
некоторого множества 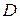 . Тогда ее производную
. Тогда ее производную 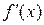 можно рассматривать как функцию, определенную на множестве
можно рассматривать как функцию, определенную на множестве 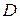 . В свою очередь функция
. В свою очередь функция 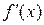 может в некоторых точках множества
может в некоторых точках множества 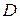 иметь производную. В этом случае производной второго порядка (второй производной) называется производная от производной
иметь производную. В этом случае производной второго порядка (второй производной) называется производная от производной 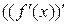 . Для второй производной функции
. Для второй производной функции  в точке x применяются обозначения:
в точке x применяются обозначения:
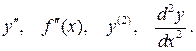
Аналогично определяются производные 3-го, 4-го, и т.д. порядков.
Производной первого порядка (или первой производной) считается 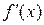 .
.
Примеры решения типовых задач
Пример 1. Найти вторую производную функции 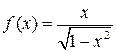 .
.
Решение. Сначала найдем 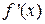 и обязательно упростим полученное выражение:
и обязательно упростим полученное выражение:
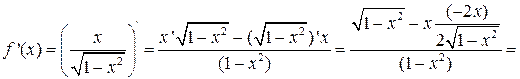
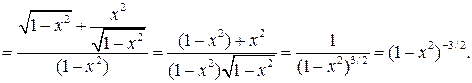
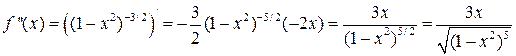 .
.
Пример 2. Найти производную второго порядка 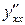 от функции, заданной параметрически:
от функции, заданной параметрически: 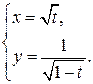 .
.
Решение. Найдем производную первого порядка:
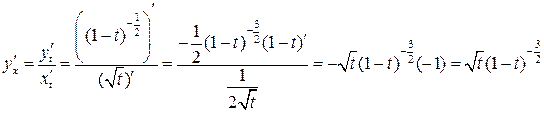 ;
;
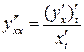 ;
; 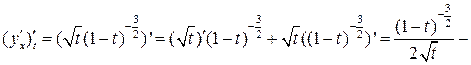
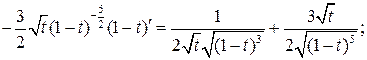
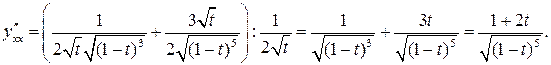
Пример 3. Найти производную n- го порядка: 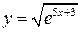 .
.
Решение. Найдем последовательно несколько производных высших порядков:
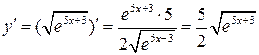 ;
;
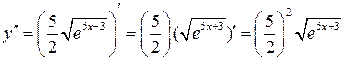 ;
;
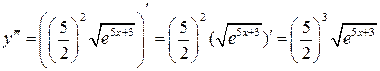 .
.
И так далее. Выведем формулу для n- го члена получившейся последовательности 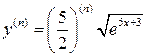 .
.
 2015-10-22
2015-10-22 474
474








