Пример 1. Составить уравнение нормали и уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
Решение. Уравнение касательной к кривой  в точке
в точке  имеет вид:
имеет вид:  . Уравнение нормали имеет вид:
. Уравнение нормали имеет вид:  .
.
Найдем производную функции в точке с абсциссой  .
.


 .
.
Запишем уравнения касательной к кривой  в точке с абсциссой
в точке с абсциссой  :
:  или
или  . Уравнение нормали в этой же точке:
. Уравнение нормали в этой же точке:  или
или  .
.
Пример 2. Составить уравнения касательной и нормали к эллипсу 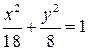 в точке
в точке  .
.
Решение. Находим производную неявной функции  :
:
 , откуда
, откуда  ,
,  . Подставляя значения
. Подставляя значения  ,
,  ,
,  в формулы уравнений касательной
в формулы уравнений касательной  и нормали
и нормали  , получим
, получим  или
или  – уравнение касательной;
– уравнение касательной;  или
или  – уравнение нормали.
– уравнение нормали.
4.Дифференциал. Приближенные вычисления с помощью
дифференциала
Если для любого достаточно малого 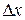 выполняется равенство
выполняется равенство  , где
, где  - постоянная,
- постоянная,  - бесконечно малая функция при
- бесконечно малая функция при  , то функция
, то функция 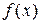 называется дифференцируемой в точке
называется дифференцируемой в точке  . Главная линейная часть приращения называют дифференциалом функции в точке
. Главная линейная часть приращения называют дифференциалом функции в точке  и обозначают в виде
и обозначают в виде
 .
.
Подчеркнем, что дифференциал – это линейная функция от  , бесконечно малая при
, бесконечно малая при  .
.
Теорема. Для того чтобы функция  имела производную
имела производную  , необходимо и достаточно, чтобы эта функция была дифференцируемой в точке
, необходимо и достаточно, чтобы эта функция была дифференцируемой в точке  , при этом
, при этом  .
.
На рис. 2 изображен график некоторой дифференцируемой функции  в точке
в точке  . Точки
. Точки  и
и 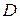 на графике функции имеют соответственно координаты
на графике функции имеют соответственно координаты  и
и 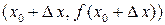 .
.

Выражения  геометрически означают длины следующих отрезков:
геометрически означают длины следующих отрезков:  . Треугольник
. Треугольник  ограничен горизонтальной линией
ограничен горизонтальной линией  , вертикальной линией
, вертикальной линией 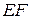 и касательной
и касательной  к графику функции в точке
к графику функции в точке  . В силу геометрического смысла производной имеем:
. В силу геометрического смысла производной имеем:  ; но тогда
; но тогда  есть длина отрезка
есть длина отрезка 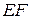 . Таким образом, с геометрической точки зрения дифференциал равен приращению ординаты касательной от точки
. Таким образом, с геометрической точки зрения дифференциал равен приращению ординаты касательной от точки  до точки
до точки  .
.
Заметим, что разделение приращения функции 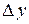 на две части:
на две части: 
 соответствует разделению отрезка
соответствует разделению отрезка  :
: 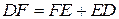 . Длина отрезка
. Длина отрезка 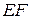 , как уже отмечалось, равна значению дифференциала, а длина отрезка
, как уже отмечалось, равна значению дифференциала, а длина отрезка  – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем  . Действительно, из рисунка видно, что доля
. Действительно, из рисунка видно, что доля  в отрезке
в отрезке  стремится к нулю при
стремится к нулю при  .
.
В равенстве  функция
функция 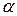 является б.м.ф. более высокого порядка, чем
является б.м.ф. более высокого порядка, чем  , следовательно, имеет смысл говорить о приближенных равенствах (при малых
, следовательно, имеет смысл говорить о приближенных равенствах (при малых 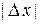 ):
):
 , или
, или  .
.
Формула  важна в задачах, когда известны значения функции
важна в задачах, когда известны значения функции 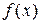 и ее производной
и ее производной 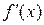 в точке
в точке  и требуется вычислить значение функции
и требуется вычислить значение функции 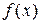 в некоторой близкой к
в некоторой близкой к  точке
точке 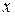 .
.
Примеры решения типовых задач
Пример 1. Найти дифференциал функции 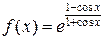 .
.
Решение. Сначала найдем первую производную исходной функции:
 Далее в силу равенства
Далее в силу равенства  получим
получим  .
.
Пример 2. Найти дифференциал функции, заданной неявно  .
.
Решение. Найдем дифференциал обеих частей равенства. Получим  . Отсюда выразим дифференциал
. Отсюда выразим дифференциал  :
:
 .
.
Пример 3. Вычислить приближенно значение  .
.
Решение. Воспользуемся формулой  . Для этого определим функцию
. Для этого определим функцию  и положим
и положим  ,
,  или в радианах
или в радианах  и
и  .
.
Тогда, учитывая, что  , получим
, получим
 , или
, или
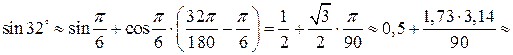

Для сравнения: имеет место равенство  с четырьмя верными знаками.
с четырьмя верными знаками.
Пример 4. Вычислить приближенно  .
.
Решение. Рассмотрим функцию 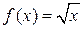 и выберем
и выберем  ,
,  . Найдем:
. Найдем:
 .
.
Тогда 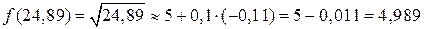 . Для сравнения: приближенно
. Для сравнения: приближенно 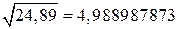 с точностью до 9-го знака после запятой.
с точностью до 9-го знака после запятой.
Правило Лопиталя
Это правило нахождения некоторых пределов функций при помощи производных. Правило Лопиталя задается следующей теоремой.
Теорема. Пусть 1) функции 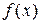 и
и  дифференцируемы в некоторой проколотой окрестности точки
дифференцируемы в некоторой проколотой окрестности точки  , 2)
, 2) 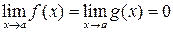 (или
(или  ), 3)
), 3)  и
и 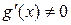 в этой окрестности. Тогда, если существует
в этой окрестности. Тогда, если существует  , то существует
, то существует  и верно равенство
и верно равенство
 .
.
Замечание. Теорема верна и для случая  (
( ).
).
Замечание. Теорема верна и для случая 
Замечание. Из условий теоремы следует, что функция  является неопределенностью вида
является неопределенностью вида 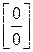 (или
(или  ) при
) при  , следовательно, теорема позволяет в некоторых случаях раскрыть эти неопределенности.
, следовательно, теорема позволяет в некоторых случаях раскрыть эти неопределенности.
Часто правило Лопиталя применяется повторно следующим образом. Пусть при выполнении условий 1) – 3) теоремы  является неопределенностью вида
является неопределенностью вида 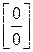 (или
(или  ). Тогда правило Лопиталя применяется повторно к
). Тогда правило Лопиталя применяется повторно к  и т. д. Если после нескольких повторных применений правила будет получено конечное или бесконечное значение предела, то оно будет равно
и т. д. Если после нескольких повторных применений правила будет получено конечное или бесконечное значение предела, то оно будет равно  .
.
Для раскрытия неопределенностей типа  необходимо преобразовать соответствующее произведение
необходимо преобразовать соответствующее произведение  , где
, где  и
и  , например,
, например,  (вид
(вид 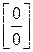 ) или
) или  (вид
(вид  ).
).
В случае неопределенности вида  необходимо преобразовать соответствующую разность
необходимо преобразовать соответствующую разность  , где
, где  и
и  , в произведение
, в произведение  и раскрыть сначала неопределенность
и раскрыть сначала неопределенность  ; если
; если  , то следует привести выражение к виду
, то следует привести выражение к виду  (вид
(вид 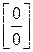 ).
).
Неопределенности видов 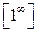 ,
,  ,
,  раскрываются с помощью предварительного логарифмирования и нахождения предела степени
раскрываются с помощью предварительного логарифмирования и нахождения предела степени  . Эти неопределенности сводятся к случаю неопределенности
. Эти неопределенности сводятся к случаю неопределенности  , при этом используется тождество
, при этом используется тождество 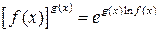 .
.
 2015-10-22
2015-10-22 1685
1685
