Геометрический смысл производной. Касательная и нормаль к кривой

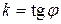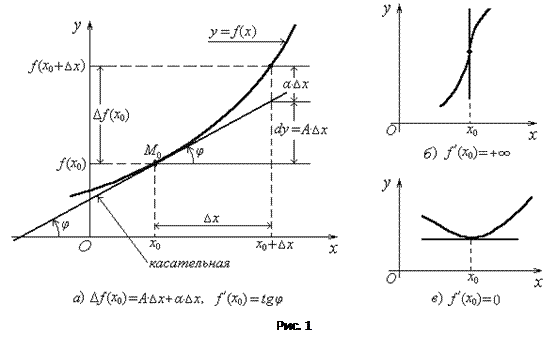
Пусть - имеет производную в точке , - точка на графике этой функции с координатами и , - угловой коэффициент касательной, проведенной к графику функции в точке , - угол наклона касательной к оси абсцисс (см. рис 1. а).

Геометрический смысл производной состоит в том, что .

Уравнение касательной к графику функции в точке имеет вид

.

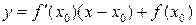Прямая, перпендикулярная к касательной и проходящая через точку касания, называется нормалью к графику функции в этой точке.

Уравнение нормали к графику функции в точке имеет вид

.

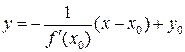Замечание. Пусть (или 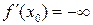). Тогда касательная к графику функции в точке параллельна оси 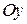, а уравнение касательной имеет вид (рис 1. б).

Замечание. Если 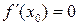, то касательная к графику функции в точке параллельна оси 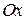(рис 1. в).