II. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Производная функции. Основные правила дифференцирования
Понятие производной
Пусть функция  определена в окрестности точки
определена в окрестности точки  ,
,  - приращение аргумента
- приращение аргумента 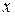 ,
,  - приращение функции.
- приращение функции.
Определение. Производнойфункции 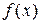 в точке
в точке  называется конечный предел
называется конечный предел  , если он существует.
, если он существует.
Производную функции 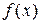 в точке
в точке  обозначают
обозначают  или
или  . Через
. Через 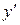 или
или  обозначают производную функции
обозначают производную функции  в точке
в точке 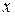 .
.
Таблица производных
1)  | 2)  |
3) 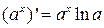 , ,  | 4)  , ,  |
5)  | 6)  |
7)  | 8)  |
9)  | 10)  |
11)  | 12)  |
Основные правила дифференцирования
Пусть  – постоянная,
– постоянная, 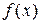 и
и  имеют производные в точке
имеют производные в точке 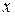 . Тогда:
. Тогда:
1.  ,
,
2.  ,
,
3. 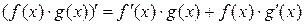 ,
,
4.  ,
, 
5. Производная сложной функции. Пусть функция  имеет производную в точке
имеет производную в точке  а функция
а функция  имеет производную в точке x. Тогда сложная функция
имеет производную в точке x. Тогда сложная функция  имеет производную в точке
имеет производную в точке 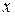 , равную
, равную
 .
.
6. Производная функции, заданной параметрически. Пусть функции 
 задают параметрически функцию
задают параметрически функцию  в окрестности точки
в окрестности точки  , функции
, функции 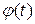 и
и  имеют производные
имеют производные  и
и 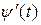 в точке
в точке  . Тогда функция
. Тогда функция  также имеет производную в точке
также имеет производную в точке 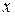 , и верна формула
, и верна формула
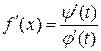 .
.
7. Производная функции, заданной неявно. Если функция задана в виде  , то производную
, то производную  можно найти по формуле:
можно найти по формуле:
 .
.
8. Дифференцирование показательно-степенной функции. Для дифференцирования показательно-степенной функции 
 , где
, где 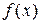 и
и  - имеют производные в точке
- имеют производные в точке 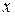 , можно представить ее в виде:
, можно представить ее в виде:
 .
.
Затем по правилу дифференцирования сложной функции получаем:
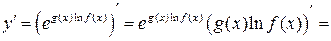
 .
.
 2015-10-22
2015-10-22 780
780







