Пример 1. Найти производную функции  по определению.
по определению.
Решение. Имеем:
 .
.
Отсюда

 .
.
Следовательно,  .
.
Пример 2. Найти производную функции  .
.
Решение. Воспользуемся правилами дифференцирования и таблицей производных:


Пример 3. Найти производную:  .
.
Решение. Воспользуемся правилами дифференцирования и таблицей производных:

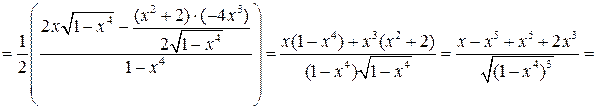
 .
.
Пример 4. Найти производную функции  .
.
Решение: Воспользуемся правилами дифференцирования:

 .
.
Пример 5. Найти производную:  .
.
Решение. При дифференцировании некоторых логарифмических выражений рациональнее предварительно упростить первоначальную функцию по свойствам логарифма:
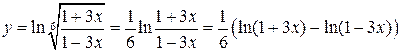 ;
;


Пример 6. Найти производную функции  .
.
Решение. По формуле

имеем

Пример 7. Используя метод логарифмического дифференцирования, вычислить производную функции  .
.
Решение. Применим метод логарифмического дифференцирования. Для этого предварительно прологарифмируем обе части данного выражения и используя свойства логарифма преобразуем правую часть.
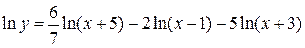 .
.
Продифференцируем обе части равенства, учитывая, что  сложная функция
сложная функция


Выражая производную искомой функция, получим

Учитывая, что  , окончательно получим
, окончательно получим 
Пример 8. Для функции, заданной параметрически, найти  .
.

Решение. Находим производные от 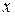 и от
и от  по параметру
по параметру 
 ,
, 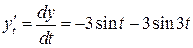 .
.
Искомую производную от  по
по 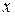 находим:
находим:
 .
.
Пример 9. Найти производную  , если
, если  .
.
Решение.
1 способ. Продифференцируем уравнение, считая переменную 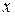 аргументом, а переменную
аргументом, а переменную  функцией
функцией  . Получим
. Получим  . Решаем уравнение относительно
. Решаем уравнение относительно  :
:
 .
.
2 способ.  . Воспользуемся формулой для нахождения производной функции, заданной неявно
. Воспользуемся формулой для нахождения производной функции, заданной неявно
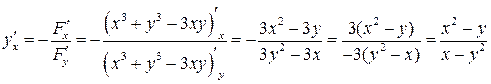 .
.
 2015-10-22
2015-10-22 465
465








