Выборочной дисперсией вариационного ряда называется средняя арифметическая квадрата отклонений вариантов от их средней арифметической.

Для дискретных вариационных рядов: 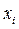 варианты,
варианты, 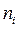 их частоты.
их частоты.
Для интервальных рядов: 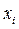 середины соответствующих интервалов,
середины соответствующих интервалов, 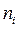 их частоты.
их частоты.
Свойства дисперсии.
1. Дисперсия постоянной равна нулю.
2. Если все варианты увеличить (уменьшить) в одно и то же число k раз, то дисперсия увеличится (уменьшится) в k2 раз.

3. Если все варианты увеличить (уменьшить) на одно и то же число k раз, то дисперсия не изменится.

4. Дисперсия равна разности между средней арифметической квадратов вариантов и квадратом средней арифметической.

5. Если ряд состоит из нескольких групп наблюдений, то общая дисперсия равна сумме средней арифметической групповых дисперсий и межгрупповой дисперсии.
 - правило сложений дисперсий.
- правило сложений дисперсий.
 - общая дисперсия
- общая дисперсия
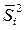 - средняя арифметическая групповых дисперсий.
- средняя арифметическая групповых дисперсий.
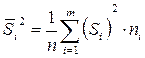
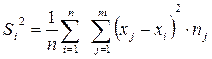

 2015-10-22
2015-10-22 1000
1000

 -
- 






