Гидростатика
Гидростатика изучает законы равновесия жидкости. Под равновесием понимается отсутствие перемещения частиц жидкости относительно стенок сосуда и друг друга. При этом если стенки сосуда неподвижны, то говорят об абсолютном равновесии, если сосуд движется, то имеют в виду равновесие жидкости.
Жидкость при этом рассматривается как непрерывная среда, заполняющая пространство полностью без пустот и промежутков.
Вследствие текучести жидкости в ней не могут действовать сосредоточенные силы, а возможно лишь действие сил, непрерывно распределенных по ее объему или по поверхности. Поэтому силы, действующие на рассматриваемые объемы жидкости и являющиеся по отношению к ним внешними силами, подразделяются на массовые и поверхностные.
Массовые силы пропорциональны массе жидкого тела или для однородной жидкости пропорциональны его объему. Это силы тяжести и силы инерции переносного движения.
Поверхностные силы непрерывно распределены по поверхности жидкости и пропорциональны величине этой поверхности.

Поверхностная сила  , действующая на площади
, действующая на площади 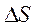 , направлена под некоторым углом к ней и силу
, направлена под некоторым углом к ней и силу  можно разложить на нормальную
можно разложить на нормальную  и тангенциальную
и тангенциальную  составляющие. Первая направлена внутрь объема и называется силой давления, а вторая силой трения.
составляющие. Первая направлена внутрь объема и называется силой давления, а вторая силой трения.
Выделив некоторую площадь,  получим следующие определения:
получим следующие определения:
- отношение силы трения к площади поверхности трения называется касательным напряжением трения

- отношение силы давления к площади поверхности воздействия называется средним гидростатическим давлением

При неограниченном уменьшении площади  участка поверхности получим соответственно касательное напряжение
участка поверхности получим соответственно касательное напряжение  и гидростатическое давление
и гидростатическое давление 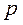 в точке:
в точке:


Гидростатическоедавление обладает двумя свойствами:
1. Всегда направлено по нормали внутрь рассматриваемого объема жидкости и является сжимающим.
2. В любой точке покоящейся жидкости не зависит от ориентации площадки, на которую оно действует, т.е. оно действует одинаково по всем направлениям.
Первое свойство доказывается тем, что если бы в покоящейся жидкости была бы касательная составляющая, то она бы вывела жидкость из состояния равновесия и она начала бы двигаться вдоль площадки, т.е. перестала быть неподвижной.
Второе свойство доказывается следующим образом:
 | Выделим в жидкости элементарный объем в виде прямоугольного тетраэдра с произвольными ребрами  . При этом произвольно наклоненная плоскость тетраэдра имеет . При этом произвольно наклоненная плоскость тетраэдра имеет |
площадь  и вдоль ее нормали
и вдоль ее нормали  действует давление
действует давление  . Сумма массовой и всех поверхностных сил, действующих на выделенный объем равна нулю. В частности, для сил, действующих вдоль оси
. Сумма массовой и всех поверхностных сил, действующих на выделенный объем равна нулю. В частности, для сил, действующих вдоль оси 

где  - проекция единичной массовой силы;
- проекция единичной массовой силы;
 - плотность жидкости.
- плотность жидкости.
Учитывая, что  , получим
, получим  .
.
При уменьшении объема до точки  приходим к равенству
приходим к равенству  . Аналогично можно получить равенство
. Аналогично можно получить равенство 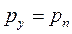 и
и  . Таким образом, в любой внутренней точке жидкости гидростатическое давление по всем направлениям одинаково.
. Таким образом, в любой внутренней точке жидкости гидростатическое давление по всем направлениям одинаково.
Основное уравнение гидростатики
Определим условия равновесия жидкости.
 | Жидкость содержится в сосуде. На ее свободную поверхность действует давление 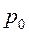 . Найдем величину гидро-статического давления . Найдем величину гидро-статического давления 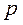 в произво-льно взятой точке М, расположенной на глубине в произво-льно взятой точке М, расположенной на глубине  . . |
У точки М, как центра, возьмем элементарную горизонтальную площадку  и построим на ней вертикальный цилиндрический объем высотой
и построим на ней вертикальный цилиндрический объем высотой  . Запишем сумму всех сил, действующих на рассматриваемый объем в вертикальном направлении:
. Запишем сумму всех сил, действующих на рассматриваемый объем в вертикальном направлении:

Отсюда, сократив  :
:

Величина 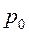 является одинаковой для всех точек объема жидкости, поэтому, учитывая второе свойство гидростатического давления можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это закон Паскаля.
является одинаковой для всех точек объема жидкости, поэтому, учитывая второе свойство гидростатического давления можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это закон Паскаля.
Обозначив через  координату точки М, а через
координату точки М, а через 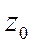 - координату свободной поверхности жидкости и учитывая, что
- координату свободной поверхности жидкости и учитывая, что  , получим
, получим
 ,
,
но так как точка М взята нами произвольно, то для всего рассматриваемого неподвижного объема жидкости

Координата  называется нивелирной высотой.
называется нивелирной высотой.
Величина  - пьезометрической высотой.
- пьезометрической высотой.
Сумма  - гидростатическим напором.
- гидростатическим напором.
Покажем то же более строго посредством интегрирования дифференциальных уравнений равновесия жидкости: для чего выделим элементарный прямоугольный объем жидкости.
 | В общем случае давление в различных точках жидкости неодинаково. Это изменение в пространстве характеризу-ется градиентами давления:  . . |
На поверхность  действует сила
действует сила  на противоположную – сила
на противоположную – сила  Таким образом на параллелепипед вдоль оси
Таким образом на параллелепипед вдоль оси  действует результирующая поверхностных сил
действует результирующая поверхностных сил  .
.
С учетом массовой силы уравнения равновесия выделенного объема по всем осям будут:

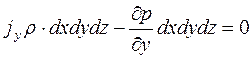

или в форме уравнений Эйлера:



Сложив уравнения и выделив полный дифференциал давления  , получим окончательную запись общего уравнения гидростатики:
, получим окончательную запись общего уравнения гидростатики:

При абсолютном покое  , поэтому общее уравнение гидростатики для этого случая:
, поэтому общее уравнение гидростатики для этого случая:
 ,
,
где  - ускорение свободного падения.
- ускорение свободного падения.
После интегрирования получим:
 или
или 
учитывая, что  -
- 
 2015-10-22
2015-10-22 929
929







