Ранее были рассмотрены примеры, в которых приводились разнообразные случайные явления (события). Как правило, их выражают числом. Представим себе, что один какой-нибудь вид случайного события имеет разное выражение числом. Например, надо определить вероятность того, что при определенной степени физической подготовки спортсмен сможет выполнить прыжок в высоту 160 см, затем 175 см, затем 180 см и т. д.
Прыжок в высоту 160 см — случайное событие, а несколько случайных событий, выраженных разными числами, называются случайными величинами. Значит, прыжок х=160 см — есть случайное событие, а прыжки х1=160 см; х2=175 см, х3=180 см и т. д. есть случайные величины.
В соответствии с определением вероятности возможно определить вероятность каждого прыжка Р(х1), Р(х2), Р(х3) и т. д.
Соотношение между случайными величинами и соответствующими им вероятностями называется законом распределения случайных величин.
Наиболее простой формой выражения такого закона является таблица, в которой каждому значению случайной величины соответствует вероятность ее появления. Такая таблица называется рядом распределения случайных величин (табл. 36):
Таблица 36
| х1 | х2 | х3 | … … | хn |
| P(x1) | P(х2) | P(х3) | … … | P(хn) |
Пример 25. На тренировочных занятиях спортсмен выполнил 50 прыжков в высоту. Из них: 32 прыжка— 160 см; 12 прыжков — 175 см и 6 прыжков — 180 см. Вероятность того, что спортсмен на соревнованиях покажет результат
P1(160 см)= 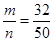 =0,64,
=0,64,
где m=32—благоприятствующие исходы для прыжка 160 см;
n=50 — равновозможные.
Вероятность того, что спортсмен на соревнованиях покажет результат
P2 (175 см)=  =0,24,
=0,24,
где m=12 благоприятствующие исходы для прыжка 175 см;
n=50 — равновозможные.
Вероятность того, что спортсмен на соревнованиях покажет результат
P3 (180 см)= 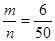 =0,12,
=0,12,
где m=6 благоприятствующие исходы для прыжка 180 см;
n=50 — равновозможные.
Составим ряд распределения случайных величин (табл. 37):
Таблица 37
| хi | 160 см | 175 см | 180 см |
| Р(хi) | 0,64 | 0,24 | 0,12 |
На основании этой таблицы данное распределение можно выразить графиком (рис. 2). Отложим на оси Х масштаб для случайных величин xi (в одной единице длины — 5 см высоты), а на оси У—масштаб для выражения вероятностей Р(хi) (в единице длины — 0,1 вероятности). Нанесем на график все три пары чисел, как результат пересечения вертикалей и горизонталей из соответствующих точек. Полученные точки соединим плавной кривой — она и будет представлять собой график данного распределения.
Естественно предположить, что чем больше рассчитать случайных величин и их вероятностей, тем более точным будет график распределения этих величин.
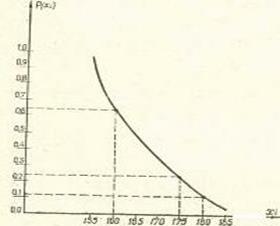
Рис. 2. Закон распределения случайных величин в примере 25
Особый интерес представляют распределения, которые имеют одинаковый график, хотя при этом рассматриваются самые разнообразные случайные величины. Такие распределения носят характер обобщающих, имеют свое выражение формулой, графиком, таблицей.
Самым распространенным среди них является нормальный закон распределения случайных величин. Его еще называют законом Гаусса по имени выдающегося немецкого математика Карла Гаусса, определившего свойства этого закона.
Внешний вид нормального закона распределения представляет собой плавную кривую, симметричную относительно средней линии (рис. 3).

Рис. 3. Нормальный закон распределения.
Среди свойств нормального закона особенно интересны такие.
1). Вершина кривой всегда точно приходится на точку  , представляющую собой среднюю арифметическую всех случайных величин.
, представляющую собой среднюю арифметическую всех случайных величин.
2). Высота кривой нормального закона характеризуется величиной среднего квадратического отклонения: чем больше этот фактор рассеивания, тем ниже и более плоско выглядит вершина, и чем меньше среднее квадратическое, тем острее и выше вершина.
3). Медиана и мода нормального распределения совпадают и равны средней арифметической
4). Площадь под всей этой кривой равна единице и выражает тот факт, что пересмотрев все случайные величины и их вероятности, получаем суммарную их вероятность максимальной: Р=1.
5). К числу замечательных свойств нормального закона относится распределение площади на участках оси х, равных ±1s, ±2s, ±3s. Знаки ± перед s возникли вследствие того, что начало оси координат можно перенести в точку  — от этого общая картина графика не нарушается. В этом случае 3s, отложенные влево от начала координат, будут с минусом, а вправо — с плюсом. Оказывается, что на участке
— от этого общая картина графика не нарушается. В этом случае 3s, отложенные влево от начала координат, будут с минусом, а вправо — с плюсом. Оказывается, что на участке  ±1s площадь под кривой составляет 0,6828 от всей площади, на участке
±1s площадь под кривой составляет 0,6828 от всей площади, на участке  ±2s=0,9545, а на участке
±2s=0,9545, а на участке  ±3s =0,9973 от всей площади. Это позволяет нам хотя бы приблизительно ориентироваться, является ли какое-либо эмпирическое распределение нормальным. Рассмотрим это подробней (рис. 4).
±3s =0,9973 от всей площади. Это позволяет нам хотя бы приблизительно ориентироваться, является ли какое-либо эмпирическое распределение нормальным. Рассмотрим это подробней (рис. 4).

Рис. 4. К правилу трех сигм.
Площадь под 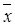 ±3s составляет 0,9973 от всей площади — это почти вся вероятность появления рассмотренных случайных величин,
±3s составляет 0,9973 от всей площади — это почти вся вероятность появления рассмотренных случайных величин,
Обратим внимание на то, что вероятность, определяемая по формуле Р(А)=  , пропорциональна числу рассматриваемых случайных событий. В связи с этим можно сказать, что под кривой нормального закона на участке
, пропорциональна числу рассматриваемых случайных событий. В связи с этим можно сказать, что под кривой нормального закона на участке 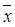 ±3s должно находиться 0,9973 всех случайных событий.
±3s должно находиться 0,9973 всех случайных событий.
Это свойство нормального закона привело к одному из практических способов, позволяющему установить нормальность закона: если на участке  ±3s содержится 0,9973 часть от объема совокупности, закон нормален.
±3s содержится 0,9973 часть от объема совокупности, закон нормален.
Пример 26. Плавание (табл. 38). хі — разность между частотой пульса после прохождения дистанции и в покое (выраженная в ударах в минуту).
Таблица 38
| xi | ni | xini | xi-x | (xi- 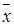 )2 )2 | (xi- 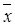 )2ni )2ni |
| 7 | 560 7 | —7 —6 —5 —4 —3 —2 +1 +2 +3 +4 +5 +6 +7 +8 | |||
| n=65 |

В соответствии с произведенной обработкой ряда методом средних величин получаем:  =82 уд/мин; 3s==8,7 уд/мин. Участок, на котором потребуется найти 0,9973 всего объема совокупности, представляет собой отрезок на оси Х от 73,3 уд/мин до 90,7 уд/мин. Сумма частот на этом участке должна быть не менее 0,9973 от всего объема совокупности n=б5 0,9973 от n=65 составляет 64,82»65. Таким образом, на отрезке от 73,3 (»73) до 90,7 (»91) должен сосредоточиться весь объем совокупности n=65.
=82 уд/мин; 3s==8,7 уд/мин. Участок, на котором потребуется найти 0,9973 всего объема совокупности, представляет собой отрезок на оси Х от 73,3 уд/мин до 90,7 уд/мин. Сумма частот на этом участке должна быть не менее 0,9973 от всего объема совокупности n=б5 0,9973 от n=65 составляет 64,82»65. Таким образом, на отрезке от 73,3 (»73) до 90,7 (»91) должен сосредоточиться весь объем совокупности n=65.
В нашем примере как раз это и наблюдается. Мы могли бы мысленно продолжить ряд вверх, где xi =74 соответствовало бы ni=0, xi=73; ni=0 и т. д. и вниз, где хi =91 соответствовало бы ni=0 и т. д. Таким образом, в нашем примере на отрезке  ±3s от 73 до 91 уд/мин сосредоточено 0,9973 часть объема совокупности, равная n=65, на основании чего можно сделать предположение, что рассмотренные случайные величины хi подвержены нормальному закону распределения.
±3s от 73 до 91 уд/мин сосредоточено 0,9973 часть объема совокупности, равная n=65, на основании чего можно сделать предположение, что рассмотренные случайные величины хi подвержены нормальному закону распределения.
Приведенное здесь правило ±3s (читается: правило плюс-минус трех сигм) представляет собой приближенный способ проверки ряда на нормальность распределения и применяется в случае первичных прикидочных расчетов. Для более точного выявления нормального распределения существуют специальные математические методы, называемые критериями согласия.
Чем бы мы ни пользовались при этом — точными или приближенными методами — конечной целью такой работы является определение, подлежит ли данное эмпирическое распределение нормальному закону или нет.
Такое выявление необходимо для того, чтобы знать, можно ли пользоваться свойствами нормального закона или нет. Ведь в случае, если эмпирическое распределение не соответствует нормальному закону, бессмысленно и даже вредно было бы пользоваться его свойствами.
Большинство задач математической статистики без преувеличения имеет принципиальное решение на основе свойств нормального закона. Это относится, в частности, и к тем задачам, которые применимы в спорте.
Следует отметить, что подавляющее большинство эмпирических распределений в спорте соответствует нормальному закону. Исследуя особенности этого закона, выдающийся русский математик А. А. Ляпунов установил, что он имеет место в тех случаях, когда на появление случайных величин оказывают влияние множество факторов одновременно, причем невозможно установить приоритет какого-либо из них.
Следует обратить внимание на то, что в спорте рассматриваются именно такие ситуации. Например, какой-либо результат спортсмена является следствием огромного количества исходных условий, из которых трудно отдать предпочтение или, наоборот, исключить из поля зрения хотя бы один из них.
Вследствие этого нормальный закон и задачи, решаемые на основании использования его свойств, имеют огромное значение в практике спортивных исследований.
 2015-10-22
2015-10-22 1352
1352
